2019年4月29日随笔档案 - canonical

2019年4月29日

可逆计算：下一代软件构造理论

原文链接：https://zhuanlan.zhihu.com/p/64004026

谨以此文庆祝清华建校108周年，及5字班本科毕业20周年

众所周知，计算机科学得以存在的基石是两个基本理论：图灵于1936年提出的图灵机理论和丘奇同年早期发表的Lambda演算理论。这两个理论奠定了所谓通用计算（Universal Computation）的概念基础，描绘了具有相同计算能力（图灵完备），但形式上却南辕北辙、大相径庭的两条技术路线。如果把这两种理论看作是上帝所展示的世界本源面貌的两个极端，那么是否存在一条更加中庸灵活的到达通用计算彼岸的中间路径?

自1936年以来，软件作为计算机科学的核心应用，一直处在不间断的概念变革过程中，各类程序语言/系统架构/设计模式/方法论层出不穷，但是究其软件构造的基本原理，仍然没有脱出两个基本理论最初所设定的范围。如果定义一种新的软件构造理论，它所引入的新概念本质上能有什么特异之处？能够解决什么棘手的问题？

本文中笔者提出在图灵机和lambda演算的基础上可以很自然的引入一个新的核心概念--可逆性，从而形成一个新的软件构造理论--可逆计算（Reversible Computation）。可逆计算提供了区别于目前业内主流方法的更高层次的抽象手段，可以大幅降低软件内在的复杂性，为粗粒度软件复用扫除了理论障碍。

可逆计算的思想来源不是计算机科学本身，而是理论物理学，它将软件看作是处于不断演化过程中的抽象实体，在不同的复杂性层次上由不同的运算规则所描述，它所关注的是演化过程中产生的微小差量如何在系统内有序的传播并发生相互作用。

本文第一节将介绍可逆计算理论的基本原理与核心公式，第二节分析可逆计算理论与组件和模型驱动等传统软件构造理论的区别和联系，并介绍可逆计算理论在软件复用领域的应用，第三节从可逆计算角度解构Docker、React等创新技术实践。

一. 可逆计算的基本原理

可逆计算可以看作是在真实的信息有限的世界中，应用图灵计算和lambda演算对世界建模的一种必然结果，我们可以通过以下简单的物理图像来理解这一点。

首先，图灵机是一种结构固化的机器，它具有可枚举的有限的状态集合，只能执行有限的几条操作指令，但是可以从无限长的纸带上读取和保存数据。例如我们日常使用的电脑，它在出厂的时候硬件功能就已经确定了，但是通过安装不同的软件，传入不同的数据文件，最终它可以自动产生任意复杂的目标输出。图灵机的计算过程在形式上可以写成

$目标输出 = 固定机器（无限复杂的输入）\\$

与图灵机相反的是，lambda演算的核心概念是函数，一个函数就是一台小型的计算机器，函数的复合仍然是函数，也就是说可以通过机器和机器的递归组合来产生更加复杂的机器。lambda演算的计算能力与图灵机等价，这意味着如果允许我们不断创建更加复杂的机器，即使输入一个常数0，我们也可以得到任意复杂的目标输出。lambda演算的计算过程在形式上可以写成

$目标输出 = 无限复杂的机器（固定输入）\\$

可以看出，以上两种计算过程都可以被表达为Y=F(X) 这样一种抽象的形式。如果我们把Y=F(X)理解为一种建模过程，即我们试图理解输入的结构以及输入和输出之间的映射关系，采用最经济的方式重建输出，则我们会发现图灵机和lambda演算都假定了现实世界中无法满足的条件。在真实的物理世界中，人类的认知总是有限的，所有的量都需要区分已知的部分和未知的部分，因此我们需要进行如下分解：

$\begin{align} Y &= F(X) \\ &= (F_0+F_1)(X_0+X_1) \tag{拆分已知和未知} \\ &= F_0(X_0)+ △ \tag{类似Taylor级数展开} \end{align}$

重新整理一下符号，我们就得到了一个适应范围更加广泛的计算模式

$Y=F(X)\oplus△\\$

除了函数运算F(X)之外，这里出现了一个新的结构运算符⊕，它表示两个元素之间的合成运算，并不是普通数值意义上的加法，同时引出了一个新的概念：差量△。△的特异之处在于，它必然包含某种负元素，F(X)与△合并在一起之后的结果并不一定是“增加”了输出，而完全可能是“减少”。

在物理学中，差量△存在的必然性以及△包含逆元这一事实完全是不言而喻的，因为物理学的建模必须要考虑到两个基本事实：

世界是“测不准”的，噪声永远存在
模型的复杂度要和问题内在的复杂度相匹配，它捕获的是问题内核中稳定不变的趋势及规律。

例如，对以下的数据

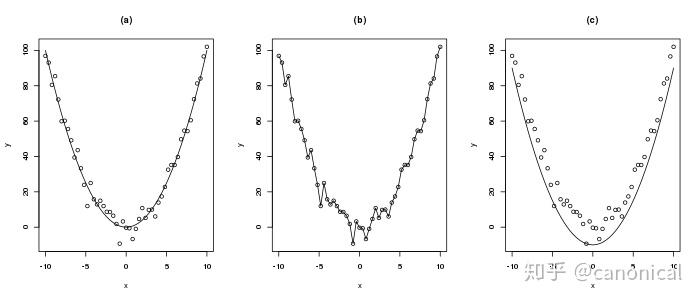
我们所建立的模型只能是类似图(a)中的简单曲线，图(b)中的模型试图精确拟合每一个数据点在数学上称之为过拟合，它难以描述新的数据，而图(c)中限制差量只能为正值则会极大的限制模型的描述精度。

以上是对Y=F(X)⊕△这一抽象计算模式的一个启发式说明，下面我们将介绍在软件构造领域落实这一计算模式的一种具体技术实现方案，笔者将其命名为可逆计算。所谓可逆计算，是指系统化的应用如下公式指导软件构造的一种技术路线

$App = Biz \quad aop\_extends \quad Generator\langle DSL\rangle \\$

App : 所需要构建的目标应用程序
DSL: 领域特定语言（Domain Specific Language），针对特定业务领域定制的业务逻辑描述语言，也是所谓领域模型的文本表示形式
Generator : 根据领域模型提供的信息，反复应用生成规则可以推导产生大量的衍生代码。实现方式包括独立的代码生成工具，以及基于元编程（Metaprogramming）的编译期模板展开
Biz : 根据已知模型推导生成的逻辑与目标应用程序逻辑之间的差异被识别出来，并收集在一起，构成独立的差量描述
aop_extends: 差量描述与模型生成部分通过类似面向切面编程（Aspect Oriented Programming）的技术结合在一起，这其中涉及到对模型生成部分的增加、修改、替换、删除等一系列操作

DSL是对关键性领域信息的一种高密度的表达，它直接指导Generator生成代码，这一点类似于图灵计算通过输入数据驱动机器执行内置指令。而如果把Generator看作是文本符号的替换生成，则它的执行和复合规则完全就是lambda演算的翻版。差量合并在某种意义上是一种很新奇的操作，因为它要求我们具有一种细致入微、无所不达的变化收集能力，能够把散布系统各处的同阶小量分离出来并合并在一起，这样差量才具有独立存在的意义和价值。同时，系统中必须明确建立逆元和逆运算的概念，在这样的概念体系下差量作为“存在”与“不存在”的混合体才可能得到表达。

现有的软件基础架构如果不经过彻底的改造，是无法有效的实施可逆计算的。正如图灵机模型孕育了C语言，Lambda演算促生了Lisp语言一样，为了有效支持可逆计算，笔者提出了一种新的程序语言X语言，它内置了差量定义、生成、合并、拆分等关键特性，可以快速建立领域模型，并在领域模型的基础上实现可逆计算。

为了实施可逆计算，我们必须要建立差量的概念。变化产生差量，差量有正有负，而且应该满足下面三条要求：

差量独立存在
差量相互作用
差量具有结构

在第三节中笔者将会以Docker为实例说明这三条要求的重要性。

可逆计算的核心是“可逆”，这一概念与物理学中熵的概念息息相关，它的重要性其实远远超出了程序构造本身，在可逆计算的方法论来源一文中，笔者会对它有更详细的阐述。

正如复数的出现扩充了代数方程的求解空间，可逆计算为现有的软件构造技术体系补充了“可逆的差量合并”这一关键性技术手段，从而极大扩充了软件复用的可行范围，使得系统级的粗粒度软件复用成为可能。同时在新的视角下，很多原先难以解决的模型抽象问题可以找到更加简单的解决方案，从而大幅降低了软件构造的内在复杂性。在第二节中笔者将会对此进行详细阐述。

软件开发虽然号称是知识密集性的工作，但到目前为止，众多一线程序员的日常中仍然包含着大量代码拷贝/粘贴/修改的机械化手工操作内容，而在可逆计算理论中，代码结构的修改被抽象为可自动执行的差量合并规则，因此通过可逆计算，我们可以为软件自身的自动化生产创造基础条件。笔者在可逆计算理论的基础上，提出了一个新的软件工业化生产模式NOP（Nop is nOt Programming），以非编程的方式批量生产软件。NOP不是编程，但也不是不编程，它强调的是将业务人员可以直观理解的逻辑与纯技术实现层面的逻辑相分离，分别使用合适的语言和工具去设计，然后再把它们无缝的粘接在一起。笔者将在另一篇文章中对NOP进行详细介绍。

可逆计算与可逆计算机有着同样的物理学思想来源，虽然具体的技术内涵并不一致，但它们目标却是统一的。正如云计算试图实现计算的云化一样，可逆计算和可逆计算机试图实现的都是计算的可逆化。

二. 可逆计算对传统理论的继承和发展

（一）组件（Component）

软件的诞生源于数学家研究希尔伯特第十问题时的副产品，早期软件的主要用途也是数学物理计算，那时软件中的概念无疑是抽象的、数学化的。随着软件的普及，越来越多应用软件的研发催生了面向对象和组件化的方法论，它试图弱化抽象思维，转而贴近人类的常识，从人们的日常经验中汲取知识，把业务领域中人们可以直观感知的概念映射为软件中的对象，仿照物质世界的生产制造过程从无到有、从小到大，逐步拼接组装实现最终软件产品的构造。

像框架、组件、设计模式、架构视图等软件开发领域中耳熟能详的概念，均直接来自于建筑业的生产经验。组件理论继承了面向对象思想的精华，借助可复用的预制构件这一概念，创造了庞大的第三方组件市场，获得了空前的技术和商业成功，即使到今天仍然是最主流的软件开发指导思想。但是，组件理论内部存在着一个本质性的缺陷，阻碍了它把自己的成功继续推进到一个新的高度。

我们知道，所谓复用就是对已有的制成品的重复使用。为了实现组件复用，我们需要找到两个软件中的公共部分，把它分离出来并按照组件规范整理成标准形式。但是，A和B的公共部分的粒度是比A和B都要小的，大量软件的公共部分是比它们中任何一个的粒度都要小得多的。这一限制直接导致越大粒度的软件功能模块越难以被直接复用，组件复用存在理论上的极限。可以通过组件组装复用60%-70%的工作量，但是很少有人能超过80%，更不用说实现复用度90%以上的系统级整体复用了。

为了克服组件理论的局限，我们需要重新认识软件的抽象本质。软件是在抽象的逻辑世界中存在的一种信息产品，信息并不是物质。抽象世界的构造和生产规律与物质世界是有着本质不同的。物质产品的生产总是有成本的，而复制软件的边际成本却可以是0。将桌子从房间中移走在物质世界中必须要经过门或窗，但在抽象的信息空间中却只需要将桌子的坐标从x改为-x而已。抽象元素之间的运算关系并不受众多物理约束的限制，因此信息空间中最有效的生产方式不是组装，而是掌握和制定运算规则。

如果从数学的角度重新去解读面向对象和组件技术，我们会发现可逆计算可以被看作是组件理论的一个自然扩展。

面向对象 : 不等式 A > B
组件 : 加法 A = B + C
可逆计算 : 差量 Y = X + △Y

面向对象中的一个核心概念是继承：派生类从基类继承，自动具有基类的一切功能。例如老虎是动物的一种派生类，在数学上，我们可以说老虎(A)这个概念所包含的内容比动物(B)这个概念更多，老虎>动物（即A>B）。据此我们可以知道，动物这个概念所满足的命题，老虎自然满足，例如动物会奔跑，老虎必然也会奔跑（ P(B) -> P(A) ）。程序中所有用到动物这一概念的地方都可以被替换为老虎（Liscov代换原则）。这样通过继承就将自动推理关系引入到软件领域中来，在数学上这对应于不等式，也就是一种偏序关系。

面向对象的理论困境在于不等式的表达能力有限。对于不等式A > B，我们知道A比B多，但是具体多什么，我们并没有办法明确的表达出来。而对于 A > B， D > E这样的情况，即使多出来的部分一模一样，我们也无法实现这部分内容的重用。组件技术明确指出"组合优于继承"，这相当于引入了加法

$A=B+C\\ D=E+C$

这样就可以抽象出组件C进行重用。

沿着上述方向推演下去，我们很容易确定下一步的发展是引入“减法”，这样才可以把 A = B + C看作是一个真正的方程，通过方程左右移项求解出

$B=A-C=A+(-C)\\$

通过减法引入的“负组件”是一个全新的概念，它为软件复用打开了一扇新的大门。

假设我们已经构建好了系统 X = D + E + F，现在需要构建 Y = D + E + G。如果遵循组件的解决方案，则需要将X拆解为多个组件，然后更换组件F为G后重新组装。而如果遵循可逆计算的技术路线，通过引入逆元 -F，我们立刻得到

$Y = X-F+G=X+(-F+G)=X+△Y\\$

在不拆解X的情况下，通过直接追加一个差量△Y，即可将系统X转化为系统Y。

组件的复用条件是“相同方可复用”，但在存在逆元的情况下，具有最大颗粒度的完整系统X在完全不改的情况下直接就可以被复用，软件复用的范围被拓展为“相关即可复用”，软件复用的粒度不再有任何限制。组件之间的关系也发生了深刻的变化，不再是单调的构成关系，而成为更加丰富多变的转化关系。

Y = X + △Y 这一物理图像对于复杂软件产品的研发具有非常现实的意义。X可以是我们所研发的软件产品的基础版本或者说主版本，在不同的客户处部署实施时，大量的定制化需求被隔离到独立的差量△Y中，这些定制的差量描述单独存放，通过编译技术与主版本代码再合并到一起。主版本的架构设计和代码实现只需要考虑业务领域内稳定的核心需求，不会受到特定客户处偶然性需求的冲击，从而有效的避免架构腐化。主版本研发和多个项目的实施可以并行进行，不同的实施版本对应不同的△Y，互不影响，同时主版本的代码与所有定制代码相互独立，能够随时进行整体升级。

（二）模型驱动架构（Model Driven Architecture)

模型驱动架构（MDA）是由对象管理组织（Object Management Group，OMG）在2001年提出的软件架构设计和开发方法，它被看作是软件开发模式从以代码为中心向以模型为中心转变的里程碑，目前大部分所谓软件开发平台的理论基础都与MDA有关。

MDA试图提升软件开发的抽象层次，直接使用建模语言（例如Executable UML）作为编程语言，然后通过使用类似编译器的技术将高层模型翻译为底层的可执行代码。在MDA中，明确区分应用架构和系统架构，并分别用平台无关模型PIM（Platform Independent Model）和平台相关模型PSM（Platform Specific Model）来描述它们。PIM反映了应用系统的功能模型，它独立于具体的实现技术和运行框架，而PSM则关注于使用特定技术（例如J2EE或者dotNet）实现PIM所描述的功能，为PIM提供运行环境。

使用MDA的理想场景是，开发人员使用可视化工具设计PIM，然后选择目标运行平台，由工具自动执行针对特定平台和实现语言的映射规则，将PIM转换为对应的PSM，并最终生成可执行的应用程序代码。基于MDA的程序构造可以表述为如下公式

$App=Transformer(PIM)\\$

MDA的愿景是像C语言取代汇编那样最终彻底消灭传统编程语言。但经历了这么多年发展之后，它仍未能够在广泛的应用领域中展现出相对于传统编程压倒性的竞争优势。

事实上，目前基于MDA的开发工具在面对多变的业务领域时，总是难掩其内在的不适应性。根据本文第一节的分析，我们知道建模必须要考虑差量。而在MDA的构造公式中，左侧的App代表了各种未知需求，而右侧的Transformer和PIM的设计器实际上都主要由开发工具厂商提供，未知=已知这样一个方程是无法持久保持平衡的。

目前，工具厂商的主要做法是提供大而全的模型集合，试图事先预测用户所有可能的业务场景。但是，我们知道“天下没有免费的午餐”，模型的价值在于体现了业务领域中的本质性约束，没有任何一个模型是所有场景下都最优的。预测需求会导致出现一种悖论: 模型内置假定过少，则无法根据用户输入的少量信息自动生成大量有用的工作，也无法防止用户出现误操作，模型的价值不明显，而如果反之，模型假定很多，则它就会固化到某个特定业务场景，难以适应新的情况。

打开一个MDA工具的设计器，我们最经常的感受是大部分选项都不需要，也不知道是干什么用的，需要的选项却到处找也找不到。

可逆计算对MDA的扩展体现为两点：

可逆计算中Generator和DSL都是鼓励用户扩充和调整的，这一点类似于面向语言编程（Language-oriented programming）。
存在一个额外的差量定制机会，可以对整体生成结果进行精确的局部修正。

在笔者提出的NOP生产模式中，必须要包含一个新的关键组件：设计器的设计器。普通的程序员可以利用设计器的设计器快速设计开发自己的领域特定语言（DSL）及其可视化设计器，同时可以通过设计器的设计器对系统中的任意设计器进行定制调整，自由的增加或者删除元素。

（三）面向切面编程（Aspect Oriented Programming)

面向切面（AOP）是与面向对象（OOP）互补的一种编程范式，它可以实现对那些横跨多个对象的所谓横切关注点（cross-cutting concern）的封装。例如，需求规格中可能规定所有的业务操作都要记录日志，所有的数据库修改操作都要开启事务。如果按照面向对象的传统实现方式，需求中的一句话将会导致众多对象类中陡然膨胀出现大量的冗余代码，而通过AOP，这些公共的“修饰性”的操作就可以被剥离到独立的切面描述中。这就是所谓纵向分解和横向分解的正交性。

AOP本质上是两个能力的组合：

在程序结构空间中定位到目标切点（Pointcut）
对局部程序结构进行修改，将扩展逻辑（Advice)编织(Weave)到指定位置。

定位依赖于存在良好定义的整体结构坐标系（没有坐标怎么定位？），而修改依赖于存在良好定义的局部程序语义结构。目前主流的AOP技术的局限性在于，它们都是在面向对象的语境下表达的，而领域结构与对象实现结构并不总是一致的，或者说用对象体系的坐标去表达领域语义是不充分的。例如，申请人和审批人在领域模型中是需要明确区分的不同的概念，但是在对象层面却可能都对应于同样的Person类，使用AOP的很多时候并不能直接将领域描述转换为切点定义和Advice实现。这种限制反映到应用层面，结果就是除了日志、事务、延迟加载、缓存等少数与特定业务领域无关的“经典”应用之外，我们找不到AOP的用武之地。

可逆计算需要类似AOP的定位和结构修正能力，但是它是在领域模型空间中定义这些能力的，因而大大扩充了AOP的应用范围。特别是，可逆计算中领域模型自我演化产生的结构差量△能够以类似AOP切面的形式得到表达。

我们知道，组件可以标识出程序中反复出现的“相同性”，而可逆计算可以捕获程序结构的“相似性”。相同很罕见，需要敏锐的甄别，但是在任何系统中，有一种相似性都是唾手可得的，即动力学演化过程中系统与自身历史快照之间的相似性。这种相似性在此前的技术体系中并没有专门的技术表达形式。

通过纵向和横向分解，我们所建立的概念之网存在于一个设计平面当中，当设计平面沿着时间轴演化时，很自然的会产生一个“三维”映射关系：后一时刻的设计平面可以看作是从前一时刻的平面增加一个差量映射（定制）而得到，而差量是定义在平面的每一个点上的。这一图像类似于范畴论（Category Theory）中的函子（Functor）概念，可逆计算中的差量合并扮演了函子映射的角色。因此，可逆计算相当于扩展了原有的设计空间，为演化这一概念找到了具体的一种技术表现形式。

（四）软件产品线（Software Product Line）

软件产品线理论源于一个洞察，即在一个业务领域中，很少有软件系统是完全独特的，大量的软件产品之间存在着形式和功能的相似性，可以归结为一个产品家族，把一个产品家族中的所有产品（已存在的和尚未存在的）作为一个整体来研究、开发、演进，通过科学的方法提取它们的共性，结合有效的可变性管理，就有可能实现规模化、系统化的软件复用，进而实现软件产品的工业化生产。

软件产品线工程采用两阶段生命周期模型，区分领域工程和应用工程。所谓领域工程，是指分析业务领域内软件产品的共性，建立领域模型及公共的软件产品线架构，形成可复用的核心资产的过程，即面向复用的开发（development for reuse）。而应用工程，其实质是使用复用来开发（ development with reuse），也就是利用已经存在的体系架构、需求、测试、文档等核心资产来制造具体应用产品的生产活动。

卡耐基梅隆大学软件工程研究所（CMU-SEI）的研究人员在2008年的报告中宣称软件产品线可以带来如下好处：

提升10倍以上生产率
提升10倍以上产品质量
缩减60%以上成本
缩减87%以上人力需求
缩减98%以上产品上市时间
进入新市场的时间以月计，而不是年

软件产品线描绘的理想非常美好：复用度90%以上的产品级复用、随需而变的敏捷定制、无视技术变迁影响的领域架构、优异可观的经济效益等等。它所存在的唯一问题就是如何才能做到？尽管软件产品线工程试图通过综合利用所有管理的和技术的手段，在组织级别策略性的复用一切技术资产（包括文档、代码、规范、工具等等），但在目前主流的技术体制下，发展成功的软件产品线仍然面临着重重困难。

可逆计算的理念与软件产品线理论高度契合，它的技术方案为软件产品线的核心技术困难---可变性管理带来了新的解决思路。在软件产品线工程中，传统的可变性管理主要是适配、替换和扩展这三种方式：

这三种方式都可以看作是向核心架构补充功能。但是可复用性的障碍不仅仅是来自于无法追加新的功能，很多时候也在于无法屏蔽原先已经存在的功能。传统的适配技术等要求接口一致匹配，是一种刚性的对接要求，一旦失配必将导致不断向上传导应力，最终只能通过整体更换组件来解决问题。可逆计算通过差量合并为可变性管理补充了“消除”这一关键性机制，可以按需在领域模型空间中构建出柔性适配接口，从而有效的控制变化点影响范围。

可逆计算中的差量虽然也可以被解释为对基础模型的一种扩展，但是它与插件扩展技术之间还是存在着明显的区别。在平台-插件这样的结构中，平台是最核心的主体，插件依附于平台而存在，更像是一种补丁机制，在概念层面上是相对次要的部分。而在可逆计算中，通过一些形式上的变换，我们可以得到一个对称性更高的公式：

$A = B \oplus G(D) \equiv (B，D) \\$

如果把G看作是一种相对不变的背景知识，则形式上我们可以把它隐藏起来，定义一个更加高级的“括号”运算符，它类似于数学中的“内积”。在这种形式下，B和D是对偶的，B是对D的补充，而D也是对B的补充。同时，我们注意到G(D)是模型驱动架构的体现，模型驱动之所以有价值就在于模型D中发生的微小变化，可以被G放大为系统各处大量衍生的变化，因此G(D)是一种非线性变换，而B是系统中去除D所对应的非线性因素之后剩余的部分。当所有复杂的非线性影响因素都被剥离出去之后，最后剩下的部分B就有可能是简单的，甚至能够形成一种新的可独立理解的领域模型结构(可以类比声波与空气的关系，声波是空气的扰动，但是不用研究空气本体，我们就可以直接用正弦波模型来描述声波)。

A = (B,D)的形式可以直接推广到存在更多领域模型的情况

$A = (B,D,E,F, ...) \\$

因为B、D、E等概念都是某种DSL所描述的领域模型，因此它们可以被解释为A投影到特定领域模型子空间所产生的分量，也就是说，应用A可以被表示为一个“特征向量”（Feature Vector），例如

$应用A = (Biz,权限,流程,报表,...) \\$

与软件产品线中常用的面向特征编程（Feature Oriented Programming）相比，可逆计算的特征分解方案强调领域特定描述，特征边界更加明确，特征合成时产生的概念冲突更容易处理。

特征向量本身构成更高维度的领域模型，它可以被进一步分解下去，从而形成一个模型级列，例如定义

$D' \equiv [B，D]\ G'(D')\equiv B\oplus G(D)\\$

, 并且假设D'可以继续分解

$D'=V\oplus M(U)=M'(U') \\$

，则可以得到

$\begin{align} A &= B ⊕ G(D) \\ &= G'(D') \\ &= G'(M'(U'))\\ &= G'(M'([V,U])) \\ \end{align} \\$

最终我们可以通过领域特征向量U'来描述D’，然后再通过领域特征向量D‘来描述原有的模型A。

可逆计算的这一构造策略类似于深度神经网络，它不再局限于具有极多可调参数的单一模型，而是建立抽象层级不同、复杂性层级不同的一系列模型，通过逐步求精的方式构造出最终的应用。

在可逆计算的视角下，应用工程的工作内容变成了使用特征向量来描述软件需求，而领域工程则负责根据特征向量描述来生成最终的软件。

三. 初露端倪的差量革命

（一）Docker

Docker是2013年由创业公司dotCloud开源的应用容器引擎，它可以将任何应用及其依赖的环境打包成一个轻量级、可移植、自包含的容器（Container），并据此以容器为标准化单元创造了一种新型的软件开发、部署和交付形式。

Docker一出世就秒杀了Google的亲儿子lmctfy （Let Me Contain That For You）容器技术，同时也把Google的另一个亲儿子Go语言迅速捧成了网红，之后Docker的发展更是一发而不可收拾。2014年开始一场Docker风暴席卷全球，以前所未有的力度推动了操作系统内核的变革，在众多巨头的跟风造势下瞬间引爆容器云市场，真正从根本上改变了企业应用从开发、构建到部署、运行整个生命周期的技术形态。

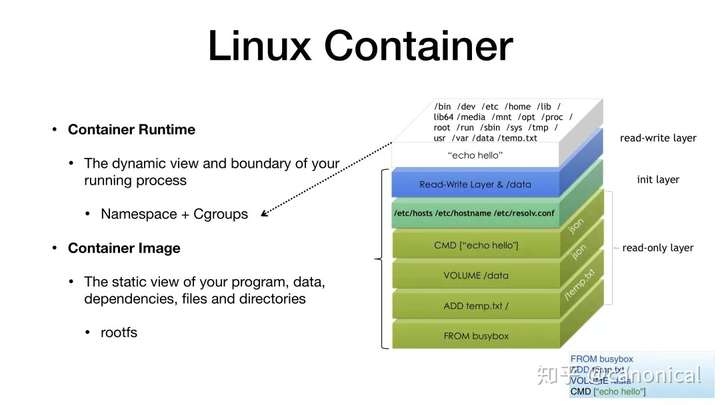
Docker技术的成功源于它对软件运行时复杂性的本质性降低，而它的技术方案可以看作是可逆计算理论的一种特例。Docker的核心技术模式可以用如下公式进行概括

$App = Docker\langle Dockerfile\rangle \quad unionfs \quad BaseImage\\$

Dockerfile是构建容器镜像的一种领域特定语言，例如

FROM ubuntu:16.04 
RUN useradd --user-group --create-home --shell /bin/bash work 
RUN apt-get update -y && apt-get install -y python3-dev 
COPY . /app RUN make /app  
ENV PYTHONPATH /FrameworkBenchmarks 
CMD python /app/app.py  
EXPOSE 8088

通过Dockerfile可以快速准确的描述容器所依赖的基础镜像，具体的构建步骤，运行时环境变量和系统配置等信息。

Docker应用程序扮演了可逆计算中Generator的角色，负责解释Dockerfile，执行对应的指令来生成容器镜像。

创造性的使用联合文件系统（Union FS），是Docker的一个特别的创新之处。这种文件系统采用分层的构造方式，每一层构建完毕后就不会再发生改变，在后一层上进行的任何修改都只会记录在自己这一层。例如，修改前一层的文件时会通过Copy-On-Write的方式复制一份到当前层，而删除前一层的文件并不会真的执行删除操作，而是仅在当前层标记该文件已删除。Docker利用联合文件系统来实现将多个容器镜像合成为一个完整的应用，这一技术的本质正是可逆计算中的aop_extends操作。

Docker的英文是码头搬运工人的意思，它所搬运的容器也经常被人拿来和集装箱做对比：标准的容器和集装箱类似，使得我们可以自由的对它们进行传输/组合，而不用考虑容器中的具体内容。但是这种比较是肤浅的，甚至是误导性的。集装箱是静态的、简单的、没有对外接口的，而容器则是动态的、复杂的、和外部存在着大量信息交互的。这种动态的复杂结构想和普通的静态物件一样封装成所谓标准容器，其难度不可同日而语。如果没有引入支持差量的文件系统，是无法构建出一种柔性边界，实现逻辑分离的。

Docker所做的标准封装其实虚拟机也能做到，甚至差量存储机制在虚拟机中也早早的被用于实现增量备份，Docker与虚拟机的本质性不同到底在什么地方？回顾第一节中可逆计算对差量三个基本要求，我们可以清晰的发现Docker的独特之处。

差量独立存在：Docker最重要的价值就在于通过容器封装，抛弃了作为背景存在（必不可少，但一般情况下不需要了解），占据了99%的体积和复杂度的操作系统层。应用容器成为了可以独立存储、独立操作的第一性的实体。轻装上阵的容器在性能、资源占用、可管理性等方面完全超越了虚胖的虚拟机。
差量相互作用：Docker容器之间通过精确受控的方式发生相互作用，可通过操作系统的namespace机制选择性的实现资源隔离或者共享。而虚拟机的差量切片之间是没有任何隔离机制的。
差量具有结构：虚拟机虽然支持增量备份，但是人们却没有合适的手段去主动构造一个指定的差量切片出来。归根结底，是因为虚拟机的差量定义在二进制字节空间中，而这个空间非常贫瘠，几乎没有什么用户可以控制的构造模式。而Docker的差量是定义在差量文件系统空间中，这个空间继承了Linux社区最丰富的历史资源。每一条shell指令的执行结果最终反映到文件系统中都是增加/删除/修改了某些文件，所以每一条shell指令都可以被看作是某个差量的定义。差量构成了一个异常丰富的结构空间，差量既是这个空间中的变换算符（shell指令），又是变换算符的运算结果。差量与差量相遇产生新的差量，这种生生不息才是Docker的生命力所在。

（二）React

2013年，也就是Docker发布的同一年，Facebook公司开源了一个革命性的Web前端框架React。React的技术思想非常独特，它以函数式编程思想为基础，结合一个看似异想天开的虚拟DOM（Virtual DOM)概念，引入了一整套新的设计模式，开启了前端开发的新大航海时代。

class HelloMessage extends React.Component {
  constructor(props) {
    super(props);
    this.state = { count: 0 };
    this.action = this.action.bind(this);
  }

  action(){
    this.setState(state => ({
      count: state.count + 1
    }));
  },

  render() {
    return (
      <button onClick={this.action}>
        Hello {this.props.name}:{this.state.count}
      </button>
    );
  }
}

ReactDOM.render(
  <HelloMessage name="Taylor" />,
  mountNode
);

React组件的核心是render函数，它的设计参考了后端常见的模板渲染技术，主要区别在于后端模板输出的是HTML文本，而React组件的Render函数使用类似XML模板的JSX语法，通过编译转换在运行时输出的是虚拟DOM节点对象。例如上面HelloMessage组件的render函数被翻译后的结果类似于

render(){
return new VNode("button", {onClick: this.action,
content: "Hello "+ this.props.name + ":" + this.state.count });
}

可以用以下公式来描述React组件： VDom = render(state)

当状态发生变化以后，只要重新执行render函数就会生成新的虚拟DOM节点，虚拟DOM节点可以被翻译成真实的HTML DOM对象，从而实现界面更新。这种根据状态重新生成完整视图的渲染策略极大简化了前端界面开发。例如对于一个列表界面，传统编程需要编写新增行/更新行/删除行等多个不同的DOM操作函数，而在React中只要更改state后重新执行唯一的render函数即可。

每次重新生成DOM视图的唯一问题是性能很低，特别是当前端交互操作众多、状态变化频繁的时候。React的神来之笔是提出了基于虚拟DOM的diff算法，可以自动的计算两个虚拟DOM树之间的差量，状态变化时只要执行虚拟Dom差量对应的DOM修改操作即可（更新真实DOM时会触发样式计算和布局计算，导致性能很低，而在JavaScript中操作虚拟DOM 的速度是非常快的）。整体策略可以表示为如下公式

$state_1=state_0\oplus action\\ \Delta VDom=render(state_1)-render(state_0)\\ \Delta Dom =Translater(\Delta VDom) \\$

显然，这一策略也是可逆计算的一种特例。

只要稍微留意一下就会发现，最近几年merge/diff/residual/delta等表达差量运算的概念越来越多的出现在软件设计领域中。比如大数据领域的流计算引擎中，流与表之间的关系可以表示为

$Table=\int \Delta Stream \\$

对表的增删改查操作可以被编码为事件流，而将表示数据变化的事件累积到一起就形成了数据表。

现代科学发端于微积分的发明，而微分的本质就是自动计算无穷小差量，而积分则是微分的逆运算，自动对无穷小量进行汇总合并。19世纪70年代，经济学经历了一场边际革命，将微积分的思想引入经济分析，在边际这一概念之上重建了整个经济学大厦。软件构造理论发展到今天，已经进入一个瓶颈，也到了应该重新认识差量的时候。

四. 结语

笔者的专业背景是理论物理学，可逆计算源于笔者将物理学和数学的思想引入软件领域的一种尝试，它最早由笔者在2007年左右提出。一直以来，软件领域对于自然规律的应用一般情况下都只限于"模拟"范畴，例如流体动力学模拟软件，虽然它内置了人类所认知的最深刻的一些世界规律，但这些规律并没有被用于指导和定义软件世界自身的构造和演化，它们的指向范围是软件世界之外，而不是软件世界自身。在笔者看来，在软件世界中，我们完全可以站在“上帝的视角”，规划和定义一系列的结构构造规律，辅助我们完成软件世界的构建。而为了完成这一点，我们首先需要建立程序世界中的“微积分”。

类似于微积分，可逆计算理论的核心是将“差量”提升为第一性的概念，将全量看作是差量的一种特例（全量=单位元+全量）。传统的程序世界中我们所表达的都只是“有”，而且是“所有”，差量只能通过全量之间的运算间接得到，它的表述和操纵都需要特殊处理，而基于可逆计算理论，我们首先应该定义所有差量概念的表达形式，然后再围绕这些概念去建立整个领域概念体系。为了保证差量所在数学空间的完备性（差量之间的运算结果仍然需要是合法的差量），差量所表达的不能仅仅是“有”，而必须是“有”和“没有”的一种混合体。也就是说差量必须是“可逆的”。可逆性具有非常深刻的物理学内涵，在基本的概念体系中内置这一概念可以解决很多非常棘手的软件构造问题。

为了处理分布式问题，现代软件开发体系已经接受了不可变数据的概念，而为了解决大粒度软件复用问题，我们还需要接受不可变逻辑的概念（复用可以看作是保持原有逻辑不变，然后增加差量描述）。目前，业内已经逐步出现了一些富有创造性的主动应用差量概念的实践，它们都可以在可逆计算的理论框架下得到统一的诠释。笔者提出了一种新的程序语言X语言，它可以极大简化可逆计算的技术实现。目前笔者已经基于X语言设计并实现了一系列软件框架和生产工具，并基于它们提出了一种新的软件生产范式（NOP）。

posted @ 2019-04-29 10:18 canonical 阅读(699) | 评论 (0) | 编辑收藏

canonical

导航

常用链接

留言簿(20)

我参与的团队

随笔分类

随笔档案

文章分类

文章档案

links

搜索

最新评论

阅读排行榜

评论排行榜