|
#
转自【http://www.cnblogs.com/coderzh/archive/2008/09/22/1296195.html 】
作者: CoderZh( CoderZh的技术博客 - 博客园)
出处: http://coderzh.cnblogs.com/
# 我这 加了些 个人理解的 说明
#encoding:UTF-8
# [递归] - 单条路 自下往上排序
def heap_adjust(data, s, m):
if 2 * s > m:return
# 声明 预设父节点位置
temp = s - 1
# [左]子节点值 大于 父节点值 : 预设父节点位置 为 左子节点位置
if data[2*s - 1] > data[temp]: temp = 2*s-1
# [右]子节点值 大于 预设父节点 : 预设父节点位置 为 右子节点位置
if 2 * s <= m - 1 and data[2*s] > data[temp]: temp = 2 * s
# 交换值 满足 堆特性 此为 [ 父节点 小于 子节点 ]
if temp <> s - 1:
data[s - 1], data[temp] = data[temp], data[s - 1]
heap_adjust(data, temp + 1, m)
def heap_sort(data):
m = len(data) / 2
# 构建 堆树
# 测试数据 [3,2,1] 数组值为 所以非底层叶节点
for i in range(m , 0, -1):
heap_adjust(data, i, len(data))
# 从堆树中 [出栈] 排序输出
# 测试数据 [5, 4, 3, 2]
data[0], data[-1] = data[-1], data[0]
for n in range(len(data) - 1, 1, -1):
heap_adjust(data, 1, n)
data[0], data[n - 1] = data[n-1], data[0]
data=[2,3,6,3,868,9,8,-1]
heap_sort(data)
print data
# [-1, 2, 3, 3, 6, 8, 9, 868]
转自 【 http://www.cppblog.com/guogangj/ 】
堆存储
 堆 入栈 复杂度为Ο(logn)
堆 入栈 复杂度为Ο(logn)
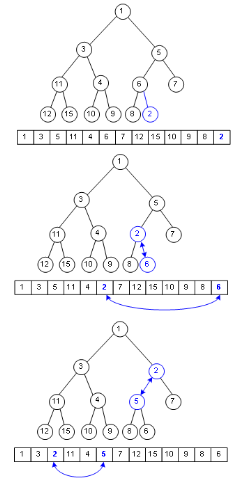 堆 出栈 Ο(logn)
堆 出栈 Ο(logn)

http://www.cnpython.org/docs/100/p_19.html
上一回我們談過了圖形介面程式的撰寫,這一次我們要討論圖形 (影像) 本身的處理,而討論的內容將會集中在 Python Imaging Library (PIL) 這一套程式庫上。
PIL
是 Python 下最有名的影像處理套件,由許多不同的模組所組成,並且提供了許多的處理功能,允許我們在簡單的 Python
程式裡進行影像的處理。使用像 PIL 許樣的程式庫套件可以幫助我們把精力集中在影像處理的工作本身,避免迷失在底層的演算法裡面。
由於影像處理牽涉到了大量的數學運算,因此 PIL 中有許多的模組是用 C 語言所寫成的,以提昇處理的效率。不過,在使用的時候,我們當然不必在意這樣的問題,只管放心地用就是了。
PIL 具備 (但不限於) 以下的能力:
- 數
十種圖檔格式的讀寫能力。常見的 JPEG, PNG, BMP, GIF, TIFF 等格式,都在 PIL 的支援之列。另外,PIL
也支援黑白、灰階、自訂調色盤、RGB true color、帶有透明屬性的 RBG true color、CMYK
及其它數種的影像模式。相當齊全。
- 基本的影像資料操作:裁切、平移、旋轉、改變尺寸、調置 (transpose)、剪下與貼上等等。
- 強化圖形:亮度、色調、對比、銳利度。
- 色彩處理。
- PIL 提供十數種濾鏡 (filter)。當然,這個數目遠遠不能與 Photoshop® 或 GIMP® 這樣的專業特效處理軟體相比;但 PIL 提供的這些濾鏡可以用在 Python 程式裡面,提供批次化處理的能力。
- PIL 可以在影像中繪圖製點、線、面、幾何形狀、填滿、文字等等。
接下來,我們開始一步一步地對 Python/PIL 的影像處理程式設計進行討論。
市面上有許多影像處理程式,一般人最常用它們來處理的工作大概就是圖檔格式轉換了;這是影像處理軟體最基本的功能,PIL 當然也要支援。
假設我們有一個 JPG 檔案,名字叫作 sample01.jpg,那麼,以下的程式會把這個檔案載入 Python:
>>> import Image
>>> im = Image.open( "sample01.jpg" )
im 這個物件是由 Image.open() 方法所產生出來的 Image 物件。我們可以用 Image 物件內的屬性來查詢關於此檔案的資訊:
>>> print im.format, im.size, im.mode
JPEG (2288, 1712) RGB
格
式字串放在 format 屬性裡,尺寸放在 size 屬性裡,而 (調色盤) 模式放在 mode
屬性裡。從以上的執行結果,可以看出來我們讀的確實是一個 JPEG 檔案,檔案的尺寸是 2288 像素寬、1712 像素高,調色盤是 RGB
全彩模式。
既然我們已經把圖檔讀入了 Python,要處理它就簡單了。利用 Image 類別的 save() 方法,可以把檔案儲存成 PIL 支援的格式:
>>> im.save( "fileout.png" )
如果圖檔很大,這會花上一點時間。Image.save() 方法會根據欲存檔的副檔名,自動判斷要存圖檔的格式 (剛剛我們用的 open() 函式也會這樣作)。
save() 可以指定存檔格式。在以下的例子裡,我們把存檔格式指定為 JPEG:
>>> im.save( "fileout.png", "JPEG" )
這時候副檔名是無所謂的。
只處理一兩個檔案的時候,使用 Python 直譯器就相當合適。然而若要處理一大群檔案,譬如把一整個目錄的 JPEG 檔轉換為 PNG 檔,那麼寫成一個程式檔會比較方便,例如:
#!/usr/bin/env python
from glob import glob
from os.path import splitext
import Image
jpglist = glob( "python_imaging_pix/*.[jJ][pP][gG]" )
for jpg in jpglist:
im = Image.open(jpg)
png = splitext(jpg)[0]+".png"
im.save(png)
print png
只要在一個放了 *.jpg 或 *.JPG 檔案的目錄裡面執行這個指令稿,它就會把所有的 JPEG 檔轉成 PNG 檔案:
$ ./convertdir.py
file0001.png
file0002.png
.
.
file9999.png
既然 PIL 會從檔名偵測常用的檔案格式,存檔時我們通常都不會指定存檔格式。
然
而,依據檔案格式的不同,save() 方法提供了不同的選項參數。以 JPEG 而言,它可以接受 quality (從 1 到 100
的整數,預設為 75)、optimize (真假值) 及 progression (真假值)。在以下的例子裡,我們以 100 的
quality 來儲存 JPEG 檔案:
>>> im.save( "quality100.jpg", quality=100 )
要訣
PIL 也支援 EPS (Encapsulate PostScript) 格式的寫入。TeX 的使用者可以利用 PIL 來簡單地把圖檔轉成 EPS 以供 TeX compiler 使用。
在了解了基本的圖檔轉換之後,我們來看看如何對影像進行尺寸方面的修改。PIL 對 Image 物件提供了 resize 方法,以執行影像的縮放工作。用我們的 sample01.jpg 檔案來當例子:
>>> im = Image.open( "sample01.jpg" )
>>> print im.size
(2288, 1712)
>>> width = 400
>>> ratio = float(width)/im.size[0]
>>> height = int(im.size[1]*ratio)
>>> nim = im.resize( (width, height), Image.BILINEAR )
>>> print nim.size
(400, 299)
>>> nim.save( "resized.jpg" )
然後我們就會得到比較小的 resized.jpg:
resize()
這個方法會傳回一個新的 Image 物件,所以舊的 Image 不會被更動。resize()
接受兩個參數,第一個用來指定變更後的大小,是一個雙元素
tuple,分別用以指定影像的寬與高;第二個參數可以省略,是用來指定變更時使用的內插法,預設是 Image.NEAREST
(取最近點),這裡我們指定為品質比較好的 Image.BILINEAR。
resize() 可以把影像放大縮小,在使用時一定要傳入寬與高。上面的程式會先限定新影像的寬,再根據舊影像的長寬比例來算出新影像的高應該是多少,最後把尺寸值傳入 resize() 去。由此可知,resize() 是允許我們不等比例縮放的:
>>> width = 400
>>> height = 100
>>> nim2 = im.resize( (width, height), Image.BILINEAR )
>>> nim2.save( "resize2wide.jpg" )
會得到形狀奇怪的縮圖:
我們可以任意改變新影像的尺寸值。
另一個常用的操作是旋轉;rotate() 方法可以用來旋轉影像。它取兩個參數,第一個參數是一個逆時針的度數,第二個參數則也是影像處理時的內插法,可省略:
>>> nim3 = nim.rotate( 45, Image.BILINEAR )
>>> nim3.save( "rotated.jpg" )
rotate() 並不會改變影像的尺寸 (dimension),所以你會看到:
出現了黑邊。如果我們想要連影像尺寸一起變動,得要改用 transpose() 方法:
>>> nim4 = nim.transpose( Image.ROTATE_90 )
>>> nim4.save( "transposed90.jpg" )
結果是:
transpose()
方法接受 Image.FLIP_LEFT_RIGHT, Image.FLIP_TOP_DOWN, ROTATE_90, ROTATE_180,
ROTATE_270 等五種參數;其中後三種的旋轉均為逆時針。rotate() 方法會對像素資料進行內插;而 transpose()
則只是轉置像素資料,所以沒有內插參數可以設定,也不會影響影像的品質。
縮放與旋轉是最常用的兩個操
作,而在其中,縮圖的製作可能是特別常用的;PIL 對縮圖提供了一個方便的 thumbnail() 方法。thumbnail() 會直接修改
Image 物件本身,所以速度能比 resize()
更快,也消耗更少的記憶體。它不接受指定內插法的參數,而且只能縮小影像,不能放大影像;用法是:
>>> im = Image.open( "sample01.jpg" )
>>> im.thumbnail( (400,100) )
>>> im.save( "thumbnail.jpg" )
>>> print im.size
(133, 100)
thumbnail()
在接受尺寸參數的時候,行為與 resize() 不同;resize() 允許我們不等比例進行縮放,但 thumbnail()
只能進行等比例縮小,並且是以長、寬中比較小的那一個值為基準。因此,上面的程式所作出的 thumbnail.jpg 變成了 133*100
的小圖片:
有了這些操作,我們可以很輕易地執行影像管理的任務。
除了可以針對圖形的尺寸作變更之外,PIL 更提供我們變更影像內容的能力。這樣,我們就不只能對影像進行管理,而能更進一步地利用程式來把影像的內容改成我們想要的樣子。
我們從「貼圖」開始:
>>> baseim = Image.open( "resized.jpg" )
>>> floatim = Image.open( "thumbnail.jpg" )
>>> baseim.paste( floatim, (150, 50) )
>>> baseim.save( "pasted.jpg" )
利用 paste() 方法,把之前作的 thumbnail.jpg 貼到 resized.jpg 裡面去:
此種用法的 paste() 方法要求兩個參數,第一是要貼上的 Image,第二是要貼上的位置。第二個參數有三種指定的方式:
- None:不指定位置與尺寸,那麼 pasted() 會假設要貼上的 Image 與被貼上的 Image 的尺寸完全相同。
- (left, upper):雙元素 tuple。pasted() 會把要貼上的 Image 的左上角對齊在指定的位置。
- (left,
upper, right, lower):四元素 tuple。paste()` 除了會把 Image
的左上角對齊外,也會對齊右下角。不過基本上這種寫法和上面那一種一樣,因為 paste()
要求要貼上的影像與這裡指定的尺寸一致,所以不可能出現不同的兩組 right, lower。
除了「貼圖」之外,我們還可以對影像的內容進行裁切:
>>> im = Image.open( "sample01.jpg" )
>>> nim = im.crop( (700, 300, 1500, 1300) )
>>> nim.thumbnail( (400,400) )
>>> nim.save( "croped.jpg" )
(因為裁切之後的圖形還是大了點,所以再縮圖一次) 得到的結果是:
crop() 接受的 box 參數指定要裁切的左、上、右、下四個邊界值,形成一個矩形。
除了剪貼之外,PIL 還可以使用內建的濾鏡 (filter) 作一些特效處理。這些濾鏡都放在 ImageFilter 模組裡面,使用前要先匯入這個模組:
>>> import ImageFilter
我們用個例子,對剛剛裁切的 "No Riding" 禁止牌作 20 次 blur (糊化),來看看 PIL 濾鏡的效果:
>>> im = Image.open( "croped.jpg" )
>>> nim = im
>>> for i in range(20): nim = nim.filter( ImageFilter.BLUR )
...
>>> nim.save( "blured.jpg" )
你應該看不出來它是 "No Riding" 了吧:
使用濾鏡的基本語法是:
newim = im.filter( ImageFilter.FILTERNAME )
其
中 FILTERNAME 是 PIL 中支援的濾鏡名稱,目前有:BLUR, CONTOUR, DETAIL, EDGE_ENHANCE,
EDGE_ENHANCE_MORE, EMBOSS, FIND_EDGES, SMOOTH, SMOOTH_MORE,
SHARPEN,此處就不一一介紹了,但建議你可以自己來把每一個濾鏡都試試看。
利用濾鏡,我們可以對同一類的影像進行相同的特效處理。當然,影像特效需要很精細的調整,在自動化作業中通常只能達到很粗略的效果;但 PIL 既然提供了,我們的自動程序就擁有更多的工具可以使用。
除了對已存在的影像進行編修之外,從零開始建立新影像也是很重要的工作。PIL 中的 ImageDraw 模組提供給我們繪製影像內容的能力。在使用 ImageDraw 之前,要先建立好空白的新影像:
>>> import ImageDraw
>>> im = Image.new( "RGB", (400,300) )
>>> draw = ImageDraw.Draw( im )
最
後建出來的 draw 是一個 ImageDraw 物件會提供各種繪製影像的方法。針對幾何圖形,draw 物件提供 arc()
(弧線)、chord() (弦)、line() (線段)、ellipse() (橢圓)、point() (點)、rectangle()
(矩形) 與 polygon() (多邊形)。不過,我們不準備討論幾何圖形的繪製;相信這些方法的使用對一般人來說應該都很直覺才是。
要訣
你
可以在指令行輸入 pydoc ImageDraw.ImageDraw.<<methodname>> 來查詢上述方法
(<<methodname>>) 的說明,譬如 pydoc ImageDraw.ImageDraw.line。
這裡要介紹的不是幾何圖形,而是文字的繪製。我們要再介紹一個模組:ImageFont,並且以實例來說明如何用 PIL 「寫字」:
>>> import Image, ImageDraw, ImageFont
>>> font = ImageFont.truetype( "
... "/usr/share/fonts/truetype/freefont/FreeMono.ttf", 24 )
>>> im = Image.new( "RGB", (400,300) )
>>> draw = ImageDraw.Draw( im )
>>> draw.text( (20,20), "TEXT", font=font )
>>> im.save( "text.jpg" )
這樣就在一個黑色底圖上用白筆寫了 "TEXT" 四個大字:
接
著一一說明剛剛作的動作。首先我們用 ImageFont 的 truetype() 函式建立了一個 TrueType 字型,大小設定為 16
點。truetype() 函式的第一個參數必須是字型檔的搜尋路徑,第二個參數是字型的點數。然後依序建立影像物件與 draw 物件。寫字的動作用
draw 物件的 text() 方法來完成,它接受兩個參數,分別是文字的左上角點、字串,另外可以用 font 選項來指定所使用的字型
(若不指定,便使用預設字型)。
在 1.1.4 版之前,PIL 是只能使用點陣字型的。現在
PIL 加入了 TrueType 向量字型的支援,對於要「寫字」的人來說實在是一大福音。對點陣字來說,想改變字型的大小得要更換字型才作得到,但
TrueType 就沒有這個限制。如果我們想要寫出兩串不同大小的文字,這樣作就可以了:
>>> largefont = ImageFont.truetype( "
... "/usr/share/fonts/truetype/freefont/FreeMono.ttf", 48 )
>>> smallfont = ImageFont.truetype( "
... "/usr/share/fonts/truetype/freefont/FreeMono.ttf", 24 )
>>> im = Image.new( "RBG", (400,300) )
>>> draw = ImageDraw.Draw( im )
>>> draw.text( (20,20), "SmallTEXT", font=smallfont )
>>> draw.text( (20,120), "LargeTEXT", font=largefont )
>>> im.save( "multitext.jpg" )
結果如:
以上就是在 PIL 裡建立文字圖形的方法。
最後,我們要說明如何改變繪製圖形 (文字) 時的顏色;繪圖時畫筆的顏色是透過 draw 物件的 ink 屬性來改變的:
>>> draw.ink = 0 + 255*256 + 0*256*256
以上會把畫筆設成綠色。ink 值必須要是一個整數,其值由色彩的 RGB 值算出。舉幾個 ink 值的例子:
- 紅色的 ink 值應設為 255(R) + 0(G)*256 + 0(B)*256*256,
- 藍色的 ink 值應設為 0(R) + 0(G)*256 + 255(B)*256*256,
- 靛色的 ink 值應設為 0(R) + 255(G)*256 + 255(B)*256*256
所設定的 ink 會影響所有後續的繪圖動作。
本文介紹了方便好用的 PIL 套件,可以讓我們用 Python 撰寫影像處理的程式。我們對圖檔的格式處理、尺寸處理以及內容的編修都作了討論,最後也說明如何從零開始創作一個影像。
對網頁程式來說,動態產生簡單的影像是特別有用的功能,可以用來補足 HTML 與 CSS 的不足之處。利用 PIL 來執行批次影像處理的工作,更能省去我們許多的操作時間。相信讀者能從其中發現它所提供的生產力。
|
|
| |
|
看第二节 - 递归树方法 :
突发奇想 能否 使用 txt 构造出 递归过程
还是有 上此提到的 递归方法 分治排序
# encoding: utf-8
arr=[]
def printTree():
ac = []
ii = 0
for r in arr :
c,ss,cc = r
sc = [' ' for i in xrange(cc*(c-1))]
for i in xrange(len(sc)) :
if i % cc == 0 : sc[i]="│"
#print "ci %s ii %s = %s "%(ci,ii,ii < ci)
if ii>=c :
sc = "".join(sc)+"├─"+ss+' '
else :
sc = "".join(sc)+"└─"+ss
ii = c
ac.append( sc )
for r in ac[::-1] :
print r
def MERGE(A,p,q,r):
#print "%s:%s - %s:%s" % (p,q+1,q+1,r+1)
if p==q : L = [A[p],10**10]
else : L = A[p:q+1]+[10**10]
if q+1==r : R = [A[r],10**10]
else : R = A[q+1:r+1]+[10*10]
i = j = 0
for k in xrange(p,r+1):
if L[i]<R[j] :
A[k]=L[i]
i+=1
else:
A[k]=R[j]
j+=1
# print "%s:%s = %s \n%s:%s = %s\n\n%s" % ( p,q, L , q+1,r,R, A)
def MERGE_SORT(A,p,r,c=1):
if p<r:
q = (p+r)/2
MERGE_SORT(A,p,q,c+1)
MERGE_SORT(A,q+1,r,c+1)
arr.append( (c,"%s - %s" % ( A[p:q+1],A[q+1:r+1]) , 3 ) )
# Debugging(A,p,q,r, sc )
MERGE(A,p,q,r)
A=[5,2,7,4,1,3,2,6]
MERGE_SORT(A,0,len(A)-1)
print A
printTree()
输出 (重下往上看 输出 排序过程 ,我就不多说了 应该很好理解了!!):
[1, 2, 2, 3, 4, 5, 6, 7]
├─[2, 4, 5, 7] - [1, 2, 3, 6]
│ ├─[1, 3] - [2, 6]
│ │ ├─[2] - [6]
│ │ └─[1] - [3]
│ ├─[2, 5] - [4, 7]
│ │ ├─[7] - [4]
│ │ └─[5] - [2]
使用参考: http://boss-wu.com/?p=627
R 语言简介

3.1 渐近号
渐近范围 f(n) = θ(g(n)) ~a=b
渐近上界 f(n) = Ο(g(n)) ~a<=b 0≤f(n)≤cg(n)
渐近下界 f(n) = Ω(g(n)) ~a>=b 0≤cg(n)≤f(n)
非渐近上界 f(n) = o(g(n)) ~a<b 0≤f(n)<cg(n)
=>lim[n<=∞](f(n)/g(n))=0
非渐近下界 f(n) = ω(g(n)) ~a>b 0≤cg(n)<f(n)
=>lim[n<=∞](f(n)/g(n))=0
渐近号使用(目前我能理解到的!):
当渐近符号出现在某个公式中时,我们将其解释为一个不在乎其名称的署名函数。
例:2n^2+3n+1 = 2n^2+θ(n) ,这种用法有助于屏蔽无关紧要的细节,如低阶项。。
∑[1≤k≤n]O(i)
3.2 标准记号和常量函数
单调性 : 单调递增 , 单调递减
# 传说中的广播体操原来是 上下取整啊 ! 呵呵
下取整,上取整 : x-1 < └X┘ <= x <= ┌X┐ < x+1
取模运算 a mod n = a-└a/n┘n
多项式 p(n) = ∑[0≤i≤d] a.i n^i
指数 (a^m)^n = a^(m*n) ; a^m*a^n = a^(m+n)
# 指数中的 特殊符号 e
# e不论对x微分几次,结果都还是e!难怪数学系学生会用e比喻坚定不移的爱情!
# 数学中的爱情符号 e 哈哈!!
e = lim[n≤∞ ](1+1/n)^n
对数
lgn = log_2(n)
lnn=log_e(n)
lg^k(n)=(lgn)^k
lg lg n = lg(lgn)
阶乘 n!
函数迭代
斐波那切
F0 = 0
F1 = 1
..
Fi = Fi-1+Fi-2
数据说明:
knnuu_...txt 文件大小 3.2G 数据格式是
user1 user2 score
..
usern userm score
我这里希望通过清洗得到:
与 user1 关系最近的 top 100 人
由于数据并非需要百分之百准确,我放弃在分隔出的数据
if len(dr)!=3 : continue
开了 7 个线程 也就是 会有 7 个 用户 的 uid 对 top 100 uid 会出现问题
对应 总用户数几十万来说 呵呵 ! 我就用这 完善7个特殊人的列表时间写个 blog 吧
并结合 linux split , awk 等 快速实现的 猥琐 多线程 哈哈!!
怎么修改下 速度提升 5倍,原来的 一小时 到 10多分钟 。。。。。
# split --bytes=500m knnuu_20091123.txt knnuu/
# ls a* | awk '{system( " python uu.py "$0" & " )}'
import bsddb,sys
db = bsddb.hashopen('../id-item-y-09-10-11.db','c')
uid = -1
arr=[]
arrsc=[]
fw = open('tc/'+sys.argv[1]+'uid-uid-sc.txt','w')
ii=0
def insertion_sort(arr,arrsc,uid,sc):
ls = min(100,len(arrsc))
if ls!=0 and sc < arrsc[ls-1] : return
for i in xrange(ls):
if arrsc[i]<=sc :
arrsc.insert(i,sc)
arr.insert(i,uid)
return
elif arrsc[i] > sc : continue
if ls < 99 :
arr.append(uid)
arrsc.append(sc)
#for row in open('knnuu_20091123.txt') :
for row in open(sys.argv[1]):
dr = row.split('\n')[0].split('\t')
if len(dr)!=3 : continue
u1,u2,strsc = dr[0],dr[1],dr[2]
sc = float(strsc)
if uid == -1 : uid = u1
if u1 != uid :
for c in xrange( min(100,len(arrsc)) ):
tu = arr[c]
ts = arrsc[c]
print >>fw,"%s\t%s\t%s" % ( db[u1],db[tu],ts )
print uid
fw.flush()
arr=[u1]
arrsc=[sc]
uid=u1
else :
insertion_sort(arr,arrsc,u2,sc)
ii+=1
#print ii,u1,uid,u2,strsc,len(arr),len(arrsc)
#if ii>10 : break
fw.close()
公式:

#数据 elt 清洗后(txt)
# 一般 user 和 item 分值化
# 比如 用户下载,收藏,试听 某item 等等
user items score
 . .
# 结果输出 (bdb)
# user item1:score1,item2:score2,item3:score3  . .
python<<EOF
import bsddb
db = bsddb.hashopen('user-items.db','c')
for row in open('user-item-sc.txt'):
row=row.split('\n')[0]
dr = row.split(':')
if not db.has_key(dr[0]) : db[dr[0]]=dr[1]+':'+dr[2]
else : db[dr[0]]=db[dr[0]]+';'+dr[1]+':'+dr[2]
db.close()
EOF
# 结果输出 (txt)
# user user score

python<<EOF
import bsddb
from math import *
db = bsddb.hashopen('user-items.db','c')
def ps(u1,u2):
um1={}
for v in db[u1].split(';') :
v=v.split(':')
um1[v[0]]=float(v[1])
um2={}
si=[]
for v in db[u2].split(';') :
v=v.split(':')
um2[v[0]]=float(v[1])
if um1.has_key( v[0] ) : si.append(v[0])
n = len(si)
if n ==0.0 :return None
sum1=sum( [um1[it] for it in si] )
sum2=sum( [um2[it] for it in si] )
sum1Sq=sum([ pow(um1[it],2) for it in si])
sum2Sq=sum([ pow(um2[it],2) for it in si])
pSum = sum( [ um1[it]*um2[it] for it in si ] )
num = pSum - (sum1*sum2/n)
den = sqrt( (sum1Sq-pow(sum1,2)/n )*( sum2Sq-pow(sum2,2)/n ) )
if den==0.0 : return None
return num/den
fc = open('user-user-sc.txt','w')
for i in xrange(1,43381):
for j in xrange(i+1,43381):
sc = ps(str(i),str(j))
if not sc == None: print >>fc, "%s\t%s\t%s" %(i,j,sc)
fc.close()
EOF
# 测试使用
python<<EOF
import bsddb
db = bsddb.hashopen('user-items.db','c')
print db['1']
EOF
25 30604 1.0
print um1['468'],um1['471']
2.0 1.0
(Pdb) print um2['468'],um2['471']
2.0 1.0
如果对大家对 推荐有一些了解,数据能到 用户与用户关系(分值化) ,是能干很多事情了。
比如:
1. 首先得到某用户相近度最高的几位活跃用户,看这几位用户在看什么,听什么 然后推荐出去
扩展:
把初始值 反过来 item user score ,然后统计出 item 和 item 之间的关系 。
当 消费某一产品 ,马上推荐出 其他的相近的产品 (時时推荐)
算法导论,一章二小节 ,分治算法
def MERGE(A,p,q,r):
print "%s:%s - %s:%s" % (p,q+1,q+1,r+1)
if p==q : L = [A[p],10**10]
else : L = A[p:q+1]+[10**10]
if q+1==r : R = [A[r],10**10]
else : R = A[q+1:r+1]+[10*10]
i = j = 0
for k in xrange(p,r+1):
if L[i]<R[j] :
A[k]=L[i]
i+=1
else:
A[k]=R[j]
j+=1
# print "%s:%s = %s \n%s:%s = %s\n\n%s" % ( p,q, L , q+1,r,R, A)
def Debugging(A,p,q,r,c):
print "%s\t%s:%s - %s:%s" % (c,p,q,q+1,r)
def MERGE_SORT(A,p,r,c=1):
if p<r:
q = (p+r)/2
MERGE_SORT(A,p,q,c+1)
MERGE_SORT(A,q+1,r,c+1)
#Debugging(A,p,q,r,c)
MERGE(A,p,q,r)
A=[5,2,7,4,1,3,2,6]
print A
MERGE_SORT(A,0,len(A)-1)
print A
结果输出》》
python 2f.py
[5, 2, 7, 4, 1, 3, 2, 6]
[1, 2, 2, 3, 4, 5, 6, 7]
分享些细节:算法并不难,但确实写了很久,调试让我很郁闷。
直到写了 def Debugging 目测:
python 2f.py
3 0:0 - 1:1
3 2:2 - 3:3
2 0:1 - 2:3
3 4:4 - 5:5
3 6:6 - 7:7
2 4:5 - 6:7
1 0:3 - 4:7
看 每层 对数组的 数组下标取值 :
在 python 中当
arr = [1,2,3,4] 我希望能取出 [2,3] 是 arr[1:3] 是最后一位不计算在内的
最典型的 arr[0,1] == [1]
这是一个很有用的 公式比如:用户消费分值权重 , 产品关联分值权重 等等
公式 
在 http://www.wolframalpha.com 中表示 :
e = (1+1/n) ^n
a*e^(-(x-b)^2/c^2)
a 峰值最大值
b 峰值x轴偏移量
c 弧度跨度
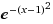 = 1*e^(-(x-1)^2/1^2)
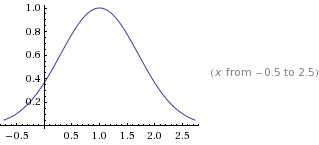
修改 峰值 a = 2
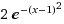
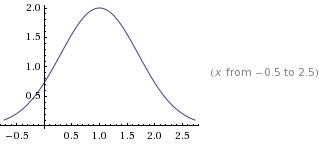
这里 就 不一一展现 b 峰值x轴偏移量 , c 弧度跨度 了 大家可以 去 wolframalpha 自己去尝试
实例1 与时间有关的递减 :
import math
def gaussian(x,peak=1.0,axis=1.0,span=1.0):
return peak*math.e**(-(x-axis)**2/(span)**2 )
跨度 c 参考:
c = 1 : 在2.5 附件急剧衰减
c = 2 : 4
c = 18 :30 # 这个数 衰减统计 一个月 不错
c = 55 :90 # 衰减统计 一个季度 不错
#简单应用
消费1次得峰值4分 浏览1次峰值2分
统计某用户季度得分
数据:在前10天浏览10次,消费1次 ,前11天浏览5次
d10 = gaussian(10,span=55.0)
d11 = gaussian(11,span=55.0)
print d10*10*2+d10*4*1+d11*5*2
#结果 33.0407089687
倒的高斯 - 实例2 :
公式 = 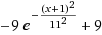
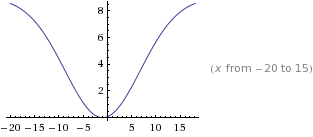
目的 与次数有关的产品分值化
#用户 对 某产品 分值化
# 比如 某用户 用过某产品 n次,我希望 n 无限大是一个 渐进某个值 而不是和 n 无限递增的
#下面的 fun 结果是 1.6 ~ 10 分值直接的区域, 也就是 传说中的 产品感兴趣 “10分制” 简易版
def gs(x,peak=9.0,axis=-2.0,span=11.0):
return "%.4f" % (-1*peak*math.e**(-(x-axis)**2/(span)**2 )+peak+1)
>>> gs(1)
'1.6451'
>>> gs(2)
'2.1148'
>>> gs(3)
'2.6800'
>>> gs(4)
'3.3161'
>>> gs(5)
'3.9970'
>>> gs(6)
'4.6969'
>>> gs(60)
'10.0000'
|