人在江湖

:: 管理

82 Posts :: 10 Stories :: 169 Comments :: 0 Trackbacks

相关概念：

相对误差（Relative Error）：绝对误差与真值的比值

所谓残差（residual error），应该是在回归时，实际y值与回归曲线得到的理论y值之间的差值。标准残差，就是各残差的标准方差。

异方差性（heteroscedasticity ）是为了保证回归参数估计量具有良好的统计性质，经典线性回归模型的一个重要假定是：总体回归函数中的随机误差项满足同方差性，即它们都有相同的方差。如果这一假定不满足，则称线性回归模型存在异方差性。

条件方差（Conditional variance）：只要把原来求方差时的概率密度函数换成条件密度函数就行了意义就是当X发生时，Y发生的方差

自相关函数（Autocorrelation function，缩写ACF）：

将一个有序的随机变量系列与其自身相比较，这就是自相关函数在统计学中的定义。每个不存在相位差的系列，都与其自身相似，即在此情况下，自相关函数值最大。如果系列中的组成部分相互之间存在相关性（不再是随机的），则由以下相关值方程所计算的值不再为零，这样的组成部分为自相关。

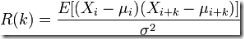
E ......... 期望值。

X_i ........ 在t(i)时的随机变量值。

μ_i ........ 在t(i)时的预期值。

X_{i + k} .... 在t(i+k)时的随机变量值。

μ_{i + k} .... 在t(i+k)时的预期值。

σ² ......... 为方差。

所得的自相关值R的取值范围为[-1,1],1为最大相关值，-1则为最大不相关值。

白噪声序列：

随机变量X（t）（t=1，2，3……），如果是由一个不相关的随机变量的序列构成的，即对于所有S不等于T，随机变量Xt和Xs的协方差均为零，则称其为纯随机过程。对于一个纯随机过程来说，若其期望和方差均为常数，则称之为白噪声过程。白噪声过程的样本实称成为白噪声序列，简称白噪声。之所以称为白噪声，是因为他和白光的特性类似，白光的光谱在各个频率上有相同的强度，白噪声的谱密度在各个频率上的值相同。

差分：差分有前向差分和后向差分。前向差分：函数的前向差分通常简称为函数的差分。对于函数，如果：

，

则称为的一阶前向差分。只所以称为前向差分是因为以x为参考点，x+1在x的前面。逆向差分：对于函数f(x)，如果：

则称为的一阶逆向差分。

时间序列的特征

非平稳性（nonstationarity，也译作不平稳性，非稳定性）：即时间序列变量无法呈现出一个长期趋势并最终趋于一个常数或是一个线性函数

波动幅度随时间变化（Time－varying Volatility）：即一个时间序列变量的方差随时间的变化而变化

虽然单独看不同的时间序列变量可能具有非稳定性，但按一定结构组合后的新的时间序列变量却可能是稳定的，即这个新的时间序列变量长期来看，会趋向于一个常数或是一个线性函数。例如，时间序列变量X(t)非稳定，但其二阶差分却可能是稳定的；时间序列变量X(t)和Y(t)非稳定，但线性组合X(t)-bY(t)却可能是稳定的。

时间序列分析通常是把各种可能发生作用的因素进行分类，传统的分类方法是按各种因素的特点或影响效果分为四大类：(1)长期趋势；(2)季节变动；(3)循环变动；(4)不规则变动。

时间序列预测法种类，

1. 简单序时平均数法算术平均法

2. 移动平均法：移动平均法是一种简单平滑预测技术，它的基本思想是：根据时间序列资料、逐项推移，依次计算包含一定项数的序时平均值，以反映长期趋势的方法。

分为简单移动平均法，加权移动平均法。一般而言，最近期的数据最能预示未来的情况，因而权重应大些。

移动平均法的优缺点

　　使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响。但移动平均法运用时也存在着如下问题：

　　1、加大移动平均法的期数（即加大n值）会使平滑波动效果更好，但会使预测值对数据实际变动更不敏感；

　　2、移动平均值并不能总是很好地反映出趋势。由于是平均值，预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动；

　　3、移动平均法要由大量的过去数据的记录。

使用移动平均法时，主要是要定下来N（用几个时期预测下个时期）是多少，实际中可以取多个N然后比相对误差。

3. 指数平滑法：所有预测方法中，指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；而指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。

指数平滑法的基本公式是：式中，

S_t--时间t的平滑值；
y_t--时间t的实际值；
S_{t − 1}--时间t-1的平滑值；
a--平滑常数，其取值范围为[0,1]；

指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1，远期实际值对本期平滑值影响程度的下降越迅速；平滑常数a越接近于 0，远期实际值对本期平滑值影响程度的下降越缓慢。由此，当时间数列相对平稳时，可取较大的a；当时间数列波动较大时，应取较小的a，以不忽略远期实际值的影响。

据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等。当时间数列无明显的趋势变化，可用一次指数平滑预测。

（一）一次指数平滑预测

　　当时间数列无明显的趋势变化，可用一次指数平滑预测。其预测公式为：

　　yt+1'=ayt+(1-a)yt' 式中，

yt+1'--t+1期的预测值，即本期（t期）的平滑值St ；
yt--t期的实际值；
yt'--t期的预测值，即上期的平滑值St-1 。

　　该公式又可以写作：yt+1'=yt'+a(yt- yt')。可见，下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。

（二）二次指数平滑预测

　　二次指数平滑是对一次指数平滑的再平滑。它适用于具线性趋势的时间数列。其预测公式为：

　　yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)

　　式中，yt= ayt-1'+(1-a)yt-1

　　显然，二次指数平滑是一直线方程，其截距为：(2yt'-yt)，斜率为：(yt'-yt) a/(1-a),自变量为预测天数。

（三）三次指数平滑预测

　　三次指数平滑预测是二次平滑基础上的再平滑。其预测公式是：

　　yt+m=(3yt'-3yt+yt)+[(6-5a)yt'-(10-8a)yt+(4-3a)yt]*am/2(1-a)2+ (yt'-2yt+yt')*a2m2/2(1-a)2

　　式中，yt=ayt-1+(1-a)yt-1

　　它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权。

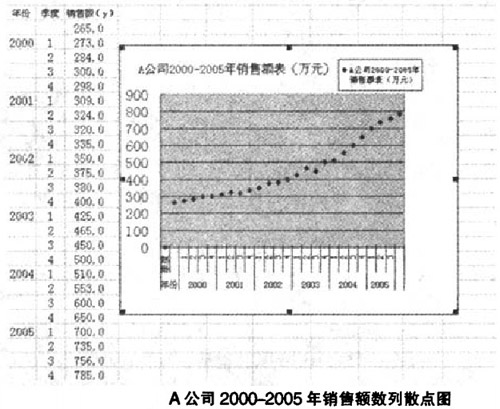
案例:指数平滑法在销售预算中的应用

　　某软件公司A为例。给出2000-2005年的历史销售资料，将数据代入指数平滑模型。预测2006年的销售额，作为销售预算编制的基础。

　　由散点图示可知。根据经验判断法。A公司2000-2005年销售额时间序列波动很大。长期趋势变化幅度较大，呈现明显且迅速的上升趋势，宜选择较大的α值，可在05-O.8间选值，以使预测模型灵敏度高些，结合试算法取0.5，0.6,0.8分别测试。经过第一次指数平滑后，数列呈现直线趋势，故选用二次指数平滑法即可。

试算结果见下表。根据偏差平方的均值(MSE)最小，即各期实际值与预测值差的平方和除以总期数．以最小值来确定理的取值的标准，经测算当α = 0.6时，MSE₁ = l445.4；当α = 0.8时，MSE₂=10783.7；当α = 0.5时，MSE₃ = 1906.1。因此选择α = 0.6来预测2006年4个季度的销售额。

　　2005年第四季度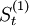 $S_t^{(1)}$ =736.8; 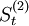$S_t^{(2)}$ =679.5;；可以求得 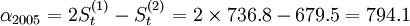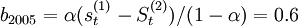$\alpha_{2005}=2S_t^{(1)}-S_t^{(2)}=2\times736.8-679.5=794.1$ ； $b_{2005}=\alpha(s_t^{(1)}-S_t^{(2)})/(1-\alpha)=0.6$ =(736.8-679.5)/0.4=85.9则预测方Y_{2005 + T} = 794.1 + 85.9T,因此，2006年第一、二、三、四季度的预测值分别为：

Y₁ = 794.1 + 85.9 = 800(万元)

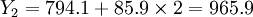$Y_2=794.1+85.9\times2=965.9$ (万元)

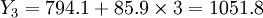$Y_3=794.1+85.9\times3=1051.8$ (万元)

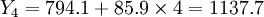$Y_4=794.1+85.9\times4=1137.7$ (万元)

　　综上所述，本案例首先根据销售历史资料，给出数列散点图。再根据散点图的特征选择二次指数平滑法，通过对α的试算，确定符合预测需要的α值，最后根据指数平滑模型计算出2006年14季度的销售预测值，作为销售预算的基础。

典型模型包括arch模型，arima模型等

arch模型：

ARCH模型的基本思想是指在以前信息集下，某一时刻一个噪声的发生是服从正态分布。该正态分布的均值为零，方差是一个随时间变化的量(即为条件异方差)。并且这个随时间变化的方差是过去有限项噪声值平方的线性组合(即为自回归)。这样就构成了自回归条件异方差模型。

　　由于需要使用到条件方差，我们这里不采用恩格尔的比较严谨的复杂的数学表达式，而是采取下面的表达方式，以便于我们把握模型的精髓。见如下数学表达：

　　Yt = βXt＋εt (1)其中，

Yt为被解释变量，
Xt为解释变量，
εt为误差项。

　　如果误差项的平方服从AR(q)过程，即εt2 =a0＋a1εt－12 ＋a2εt－22 ＋ …… ＋ aqεt－q2 ＋ηt t =1,2,3…… (2)其中，

　　ηt独立同分布，并满足E（ηt）= 0, D(ηt)= λ2 ,则称上述模型是自回归条件异方差模型。简记为ARCH模型。称序列εt 服从q阶的ARCH的过程，记作εt －ARCH(q)。为了保证εt2 为正值，要求a0 >0 ,ai ≥0 i=2,3,4… 。

　　上面（1）和（2）式构成的模型被称为回归－ARCH模型。ARCH模型通常对主体模型的随机扰动项进行建模分析。以便充分的提取残差中的信息，使得最终的模型残差ηt成为白噪声序列。

　　从上面的模型中可以看出，由于现在时刻噪声的方差是过去有限项噪声值平方的回归，也就是说噪声的波动具有一定的记忆性，因此，如果在以前时刻噪声的方差变大，那么在此刻噪声的方差往往也跟着变大；如果在以前时刻噪声的方差变小，那么在此刻噪声的方差往往也跟着变小。体现到期货市场，那就是如果前一阶段期货合约价格波动变大，那么在此刻市场价格波动也往往较大

GARCH模型是一个专门针对金融数据所量体订做的回归模型

arima模型：

Autoregressive Integrated Moving Average Model。 ARIMA（p，d，q）称为差分自回归移动平均模型，AR是自回归, p为自回归项; MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。

ARIMA模型预测的基本程序

（一）根据时间序列的散点图、自相关函数和偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律，对序列的平稳性进行识别。一般来讲，经济运行的时间序列都不是平稳序列。

　　（二）对非平稳序列进行平稳化处理。如果数据序列是非平稳的，并存在一定的增长或下降趋势，则需要对数据进行差分处理，如果数据存在异方差，则需对数据进行技术处理，直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零。

　　（三）根据时间序列模型的识别规则，建立相应的模型。若平稳序列的偏相关函数是截尾的，而自相关函数是拖尾的，可断定序列适合AR模型；若平稳序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA模型；若平稳序列的偏相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。

　　（四）进行参数估计，检验是否具有统计意义。

　　（五）进行假设检验，诊断残差序列是否为白噪声。

　　（六）利用已通过检验的模型进行预测分析。

取对数可以消除数据波动变大趋势，对数列进行一阶差分，可以消除数据增长趋势性和季节性。

一个例子：

备件消耗预测ARIMA(p,d,q)模型实质是先对非平稳的备件消耗历史数据Yt进行d（d＝0,1,dots,n）次差分处理得到新的平稳的数据序列Xt，将Xt拟合ARMA(p,q)模型，然后再将原d次差分还原，便可以得到Y_t的预测数据。其中，ARMA(p,q)的一般表达式为：

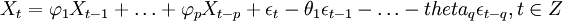$X_t=\varphi_1X_{t-1}+\ldots+\varphi_pX_{t-p}+\epsilon_t-\theta_1\epsilon_{t-1}-\ldots-theta_q\epsilon_{t-q},t\in Z$ 　　(1)

　　式中，前半部分为自回归部分，非负整数p为自回归阶数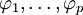， $\varphi_1,\ldots,\varphi_p$ 为自回归系数，后半部分为滑动平均部分，非负整数q为滑动平均阶数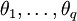， $\theta_1,\ldots,\theta_q$ 为滑动平均系数；X_t为备件消耗数据相关序列，ε_t为WN(0,σ²)。

　　当q=0时，该模型成为AR(p)模型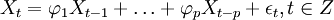： $X_t=\varphi_1X_{t-1}+\ldots+\varphi_pX_{t-p}+\epsilon_t,t\in Z$ 　　(2)

　　当p＝0时，该模型成为MA(q)模型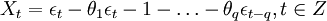： $X_t=\epsilon_t-\theta_1\epsilon_t-1-\ldots-\theta_q\epsilon_{t-q},t\in Z$ 　　(3)

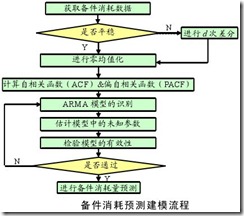
所谓零均值化处理就是取前N组（或全部）数据作为观测数据，进行零均值化处理，即：，得到一组预处理后的新序列。

SAS与arima：

sas 有proc arima. 分为三个阶段：

identification: 识别候选arima模型。

estimation and diagnositic checking: 为模型估计参数，并提供诊断统计信息帮助判断模型是否好。

forcasting: 预测未来值。

这里有一个proc arima的例子： http://www.docin.com/p-46241714.html

贴一下代码，生成data set的部分略有改动，copy&paste pdf的数据到txt中，然后批量输入data set. 方便生成data set

filename input "c:\temp\sun.txt";
data exp1;
   infile input;
   input a1 @@;
   year=intnx('year','1jan1742'd,_n_-1);
   format year year4.;
run;

proc gplot data=exp1;
symbol i=spline v=star h=2 c=green;
plot a1*year;
run;

proc arima data=exp1;
identify var=a1 nlag=24;
run;

estimate p=3;
run;

forecast lead=6 interval=year id=year out=out;
run;
proc print data=out;
run;

vcycyv:

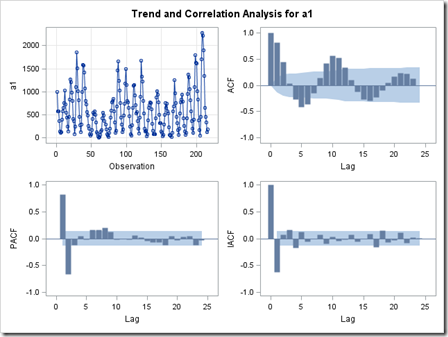
1. nlag取24，在图上看是一个w型。

2. 书上做identification步骤之后，得出结论：“观察输出结果。初步识别序列为 AR(3)模型。” 不确定这个结论是怎么得出来的，1. 怎么算截尾，怎么算拖尾？2. AR（3）里那个3是怎么出来的？对第二个问题瞎猜一下，是看ACF图观察出来三个值能推出来第四个值么？

问了学统计的同事，解答了上面两个问题，还是需要继续理解：

截尾：是指在ACF或PACF图中自相关系数和偏自相关系数在滞后的前几期内处于置信区间之外，而滞后的系数基本上都落入置信区间内，且逐渐趋于0.
拖尾：是指在ACF或PACF图中自相关系数和偏自相关系数有指数型、正弦型或震荡型衰减的波动。且都不会落入置信区间内。
至于那个3，因为PACF图上可以看出当为3时，不在置信区间内

就是那时开始不在蓝框内了

并且ACF图此时为拖尾

参考：

http://wiki.mbalib.com/wiki/%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97%E9%A2%84%E6%B5%8B%E6%B3%95

http://wiki.mbalib.com/wiki/%E7%A7%BB%E5%8A%A8%E5%B9%B3%E5%9D%87%E6%B3%95

http://wiki.mbalib.com/wiki/%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95

http://zh.wikipedia.org/wiki/%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97

http://zh.wikipedia.org/wiki/%E8%87%AA%E7%9B%B8%E5%85%B3%E5%87%BD%E6%95%B0

http://wiki.mbalib.com/wiki/ARIMA%E6%A8%A1%E5%9E%8B

http://www.docin.com/p-46241714.html

SAS help

posted on 2011-09-07 09:44 人在江湖阅读(3141) 评论(2) 编辑收藏所属分类: BI

Feedback

# re: 时间序列 2011-09-09 08:23 tb

算法很好学习了回复更多评论

# re: 时间序列 2011-09-13 18:10 -+

你疯了？回复更多评论

新用户注册刷新评论列表


只有注册用户登录后才能发表评论。




网站导航: 博客园 IT新闻知识库 C++博客博问管理
相关文章: 自录pentaho视频教程神经网络决策树 cluster聚类分析线性回归矩阵与SAS IML浅尝辄止时间序列分享读书笔记 Data Mining Concepts and Techniques Basel2模型验证二：Kendall tau Basel2模型验证一：Hosmer–Lemeshow test

人在江湖

公告

常用链接

留言簿(16)

随笔分类(90)

搜索

积分与排名

最新评论

阅读排行榜