2.2 多项式函数
看其他篇章到目录选择。
在Commons Math中的analysis.polynomials包中有所有的与多项式函数相关的类和接口定义。这一篇主要从这个包分析，来研究一下多项式函数的应用。
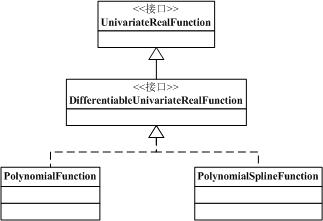
Polynomials包中没有interface的定义，下属含有5个类：PolynomialFunction、PolynomialFunctionLagrangeForm、PolynomialFunctionNewtonForm、PolynomialSplineFunction和PolynomialsUtils。其中主要的只有PolynomialFunction和PolynomialSplineFunction，正如api doc中的介绍，PolynomialFunction类是Immutable representation of a real polynomial function with real coefficients——实数多项式的表示；PolynomialSplineFunction类是Represents a polynomial spline function.——样条曲线多项式的表示。另外两个表示拉格朗日和牛顿形式的多项式函数。而PolynomialsUtils类中提供了几个构造个别（比如切比雪夫多项式）多项式的静态方法。
我觉得最常用的应该就是实数系数的多项式了，因此以PolynomialFunction类为例来进行分析。实数系数的多项式函数形如：f(x) = ax^2 + bx + c。PolynomialFunction类实现了DifferentiableUnivariateRealFunction接口，因此必须实现value()和derivative()方法，并且实现该接口也表明这是一元可微分的实数函数形式。PolynomialFunction类定义了一组final double coefficients[]作为多项式系数，其中coefficients[0]表示常数项的系数，coefficients[n]表示指数为n的x^n次项的系数。因此，这个类所表达的多项式函数是这样的：f(x)=coeff[0] + coeff[1]x + coeff[2]x^2 + … + coeff[n]x^n。它的构造方法是PolynomialFunction(double [])就是接受这样的coefficients数组作为系数输入参数来构造多项式的。这个是很好表达也很方便理解的。那么它的value(double x)方法是通过调用double evaluate(double[] coefficients, double argument)实现的，本质用Horner's Method求解多项式的值，没有什么技术难点，非常好理解的一个给定参数和函数求值过程。剩余定义的一些加减乘等操作，都是通过一个类似public PolynomialFunction add(final PolynomialFunction p)这样的结构实现的。求导数的方法derivative()是通过这样的一个微分操作实现的。见源码：
1
protected static double[] differentiate(double[] coefficients) 
{
2
int n = coefficients.length;
3
if (n < 1) {
4 throw MathRuntimeException.createIllegalArgumentException("empty polynomials coefficients array");
5
}
6 if (n == 1) {
7 return new double[]{0};
8 }
9 double[] result = new double[n - 1];
10 for (int i = n - 1; i > 0; i--) {
11 result[i - 1] = i * coefficients[i];
12 }
13 return result;
14
}
15
测试代码示例如下：
1/** *//**
2 *
3 */
4package algorithm.math;
5
6import org.apache.commons.math.ArgumentOutsideDomainException;
7import org.apache.commons.math.analysis.polynomials.PolynomialFunction;
8import org.apache.commons.math.analysis.polynomials.PolynomialSplineFunction;
9
10/** *//**
11 * @author Jia Yu
12 * @date 2010-11-21
13 */
14public class PolinomialsFunctionTest {
15
16 /** *//**
17 * @param args
18 */
19 public static void main(String[] args) {
20 // TODO Auto-generated method stub
21 polynomials();
22 System.out.println("-----------------------------------------------");
23 polynomialsSpline();
24 }
25
26 private static void polynomialsSpline() {
27 // TODO Auto-generated method stub
28 PolynomialFunction[] polynomials = {
29 new PolynomialFunction(new double[] { 0d, 1d, 1d }),
30 new PolynomialFunction(new double[] { 2d, 1d, 1d }),
31 new PolynomialFunction(new double[] { 4d, 1d, 1d }) };
32 double[] knots = { -1, 0, 1, 2 };
33 PolynomialSplineFunction spline = new PolynomialSplineFunction(knots,
34 polynomials);
35 //output directly
36 System.out.println("poly spline func is "+spline);
37 // get the value when x = 0.5
38 try {
39 System.out.println("f(0.5) = "+spline.value(0.5));
40 } catch (ArgumentOutsideDomainException e) {
41 // TODO Auto-generated catch block
42 e.printStackTrace();
43 }
44 // the number of spline segments
45 System.out.println("spline segments number is "+spline.getN());
46 // the polynomials functions
47 for(int i=0;i<spline.getN();i++){
48 System.out.println("spline:f"+i+"(x) = "+spline.getPolynomials()[i]);
49 }
50 //function derivative
51 System.out.println("spline func derivative is "+spline.derivative());
52 }
53
54 private static void polynomials() {
55 // TODO Auto-generated method stub
56 double[] f1_coeff = { 3.0, 6.0, -2.0, 1.0 };
57 double[] f2_coeff = { 1.0, 2.0, -1.0, -2.0 };
58 PolynomialFunction f1 = new PolynomialFunction(f1_coeff);
59 PolynomialFunction f2 = new PolynomialFunction(f2_coeff);
60 // output directly
61 System.out.println("f1(x) is : " + f1);
62 System.out.println("f2(x) is : " + f2);
63 // polynomial degree
64 System.out.println("f1(x)'s degree is " + f1.degree());
65 // get the value when x = 2
66 System.out.println("f1(2) = " + f1.value(2));
67 // function add
68 System.out.println("f1(x)+f2(x) = " + f1.add(f2));
69 // function substract
70 System.out.println("f1(x)-f2(x) = " + f1.subtract(f2));
71 // function multiply
72 System.out.println("f1(x)*f2(x) = " + f1.multiply(f2));
73 // function derivative
74 System.out.println("f1'(x) = " + f1.derivative());
75 System.out.println("f2''(x) = "
76 + ((PolynomialFunction) f2.derivative()).derivative());
77
78 }
79
80}
81
输出如下：
f1(x) is : 3.0 + 6.0 x - 2.0 x^2 + x^3
f2(x) is : 1.0 + 2.0 x - x^2 - 2.0 x^3
f1(x)'s degree is 3
f1(2) = 15.0
f1(x)+f2(x) = 4.0 + 8.0 x - 3.0 x^2 - x^3
f1(x)-f2(x) = 2.0 + 4.0 x - x^2 + 3.0 x^3
f1(x)*f2(x) = 3.0 + 12.0 x + 7.0 x^2 - 15.0 x^3 - 8.0 x^4 + 3.0 x^5 - 2.0 x^6
f1'(x) = 6.0 - 4.0 x + 3.0 x^2
f2''(x) = -2.0 - 12.0 x
-----------------------------------------------
poly spline func is org.apache.commons.math.analysis.polynomials.PolynomialSplineFunction@69b332
f(0.5) = 2.75
spline segments number is 3
spline:f0(x) = x + x^2
spline:f1(x) = 2.0 + x + x^2
spline:f2(x) = 4.0 + x + x^2
spline func derivative is org.apache.commons.math.analysis.polynomials.PolynomialSplineFunction@173a10f
PolynomialFunction类也是重写了toString方法和hashCode和equals方法的。
PolynomialSplineFunction类是多项式样条函数，样条是一种特殊的函数，由多项式分段定义。表示了一个由多个多项式组成的样条曲线。它的实现主要是内部定义了一个多项式函数组PolynomialFunction polynomials[]和一个样条分界节点数组double knots[]。这两个内部成员分别表示什么呢？分界节点表示整条曲线对应在x等于knots[i]的时候开始使用其他多项式样条，其构造方法public PolynomialSplineFunction(double knots[], PolynomialFunction polynomials[])完成这样的功能。
举例来说，一个多项式样条函数就是一个分段函数：
X^2+x [-1,0)
F(x) = x^2+x+2 [0,1)
X^2+x+4 [1,2)
当然，构造方法中的参数，knots[]数组必须是递增的。
可以看到，直接输出PolynomialSplineFunction是多么丑陋啊~~，因为它没有重写toString方法。同样，它的导数也是一样的丑陋。其中如果给定的值不在定义域内，value方法还抛出异常ArgumentOutsideDomainException。
最后PolynomialFunctionLagrangeForm和PolynomialFunctionNewtonForm类完成的其实是多项式插值的功能，放到下一节研究的。
相关资料：
多项式：http://zh.wikipedia.org/zh-cn/%E5%A4%9A%E9%A1%B9%E5%BC%8F%E5%87%BD%E6%95%B0#.E5.A4.9A.E9.A0.85.E5.BC.8F.E5.87.BD.E6.95.B8.E5.8F.8A.E5.A4.9A.E9.A0.85.E5.BC.8F.E7.9A.84.E6.A0.B9
样条函数：http://zh.wikipedia.org/zh-cn/%E6%A0%B7%E6%9D%A1%E5%87%BD%E6%95%B0
Horner Methods：http://mathworld.wolfram.com/HornersMethod.html
Commons math包：http://commons.apache.org/math/index.html