1. 层次聚类
层次聚类算法与之前所讲的顺序聚类有很大不同，它不再产生单一聚类，而是产生一个聚类层次。说白了就是一棵层次树。介绍层次聚类之前，要先介绍一个概念——嵌套聚类。讲的简单点，聚类的嵌套与程序的嵌套一样，一个聚类中R1包含了另一个R2，那这就是R2嵌套在R1中，或者说是R1嵌套了R2。具体说怎么算嵌套呢？聚类R1={{x1,x2},{x3},{x4,x5}嵌套在聚类R2={{x1,x2,x3},{x4,x5}}中，但并不嵌套在聚类R3={{x1,x4},{x3},{x2,x5}}中。
层次聚类算法产生一个嵌套聚类的层次，算法最多包含N步，在第t步，执行的操作就是在前t-1步的聚类基础上生成新聚类。主要有合并和分裂两种实现。我这里只讲合并，因为前一阶段正好课题用到，另外就是合并更容易理解和实现。当然分裂其实就是合并的相反过程。
令g(Ci,Cj)为所有可能的X聚类对的函数，此函数用于测量两个聚类之间的近邻性，用t表示当前聚类的层次级别。通用合并算法的伪码描述如下：
1. 初始化：
a) 选择Â0={{x1},…,{xN}}
b) 令t=0
2. 重复执行以下步骤：
a) t=t+1
b) 在Ât-1中选择一组(Ci,Cj)，满足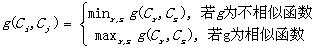
c) 定义Cq=CiÈCj，并且产生新聚类Ât=(Ât-1-{Ci,Cj})È{Cq}
直到所有向量全被加入到单一聚类中。
这一方法在t层时将两个向量合并，那么这两个向量在以后的聚类过程中的后继聚类都是相同的，也就是说一旦它们走到一起，那么以后就不会再分离……（很专一哦O(∩_∩)O~）。这也就引出了这个算法的缺点，当在算法开始阶段，若出现聚类错误，那么这种错误将一直会被延续，无法修改。在层次t上，有N-t个聚类，为了确定t+1层上要合并的聚类对，必须考虑(N-t)(N-t-1)/2个聚类对。这样，聚类过程总共要考虑的聚类对数量就是(N-1)N(N+1)/6，也就是说整个算法的时间复杂度是O(N3)。
举例来说，如果令X={x1, x2, x3, x4, x5}，其中x1=[1, 1]T, x2=[2, 1]T, x3=[5, 4]T, x4=[6, 5]T, x5=[6.5, 6]T。那么合并算法执行的过程可以用下面的图来表示。
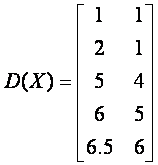
P(X)是不相似矩阵
该算法从核心过程上来讲，就是先计算出数据集中向量之间的距离，记为距离矩阵（也叫不相似矩阵）。接着通过不断的对矩阵更新，完成聚类。矩阵更新算法的伪码描述如下：
1. 初始化：
a) Â0={{x1},…,{xN}}
b) P0=P(X) (距离矩阵)
c) t=0
2. 重复执行以下步骤：
a) t=t+1
b) 合并Ci和Cj为Cq，这两个聚类满足d(Ci,Cj)=minr,s=1,…,N,r≠sd(Cr,Cs)
c) 删除第i和j行，第i和j列，同时插入新的行和列，新的行列为新合并的类Cq与所有其他聚类之间的距离值
直到将所有向量合并到一个聚类中
大家可以看到，层次聚类算法的输出结果总是一个聚类，这往往不是我们想要的，我们总希望算法在得到我们期望的结果后就停止。那么我们如何控制呢？常用的做法就是为算法限制一个阈值，矩阵更新过程中，总是将两个距离最近的聚类合并，那么我们只要加入一个阈值判断，当这个距离大于阈值时，就说明不需要再合并了，此时算法结束。这样的阈值引入可以很好的控制算法结束时间，将层次截断在某一层上。
2. 算法实现
MATLAB实现了层次聚类算法，基本语句如下：
1
X = [1 2;2.5 4.5;2 2;4 1.5;4 2.5] ;
2Y = pdist(X,'euclid');
3Z = linkage(Y,'single');
4T = cluster(Z,'cutoff',cutoff);
MATLAB还有一个简化的层次聚类版本，一句话搞定
1T = clusterdata(X,cutoff)
Java实现的版本：
1package util;
2
3import java.util.*;
4
5
public class Clusterer 
{
6
private List[] clusterList;
7 DisjointSets ds;
8 private static final int MAX = Integer.MAX_VALUE;
9 private int n;
10 private int cc;
11
12 // private double ori[] = {1,2,5,7,9,10};
13
14
public Clusterer(int num) {
15 ds = new DisjointSets(num);
16 n = num;
17 cc = n;
18 clusterList = new ArrayList[num];
19 for (int i = 0; i < n; i++)
20 clusterList[i] = new ArrayList();
21
}
22
23 public List[] getClusterList() {
24 return clusterList;
25 }
26
27 public void setClusterList(List[] clusterList) {
28 this.clusterList = clusterList;
29 }
30
31 public void output() {
32 int ind = 1;
33 for (int i = 0; i < n; i++) {
34 clusterList[ds.find(i)].add(i);
35 }
36 for (int i = 0; i < n; i++) {
37 if (clusterList[i].size() != 0) {
38 System.out.print("cluster " + ind + " :");
39 for (int j = 0; j < clusterList[i].size(); j++) {
40 System.out.print(clusterList[i].get(j) + " ");
41 }
42 System.out.println();
43 ind++;
44 }
45 }
46 }
47
48 /** *//**
49 * this method provides a hierachical way for clustering data.
50 *
51 * @param r
52 * denote the distance matrix
53 * @param n
54 * denote the sample num(distance matrix's row number)
55 * @param dis
56 * denote the threshold to stop clustering
57 */
58 public void cluster(double[][] r, int n, double dis) {
59 int mx = 0, my = 0;
60 double vmin = MAX;
61 for (int i = 0; i < n; i++) { // 寻找最小距离所在的行列
62 for (int j = 0; j < n; j++) {
63 if (j > i) {
64 if (vmin > r[i][j]) {
65 vmin = r[i][j];
66 mx = i;
67 my = j;
68 }
69 }
70 }
71 }
72 if (vmin > dis) {
73 return;
74 }
75 ds.union(ds.find(mx), ds.find(my)); // 将最小距离所在的行列实例聚类合并
76 double o1[] = r[mx];
77 double o2[] = r[my];
78 double v[] = new double[n];
79 double vv[] = new double[n];
80 for (int i = 0; i < n; i++) {
81 double tm = Math.min(o1[i], o2[i]);
82 if (tm != 0)
83 v[i] = tm;
84 else
85 v[i] = MAX;
86 vv[i] = MAX;
87 }
88 r[mx] = v;
89 r[my] = vv;
90 for (int i = 0; i < n; i++) { // 更新距离矩阵
91 r[i][mx] = v[i];
92 r[i][my] = vv[i];
93 }
94 cluster(r, n, dis); // 继续聚类，递归直至所有簇之间距离小于dis值
95 }
96
97 /** *//**
98 *
99 * @param r
100 * @param cnum
101 * denote the number of final clusters
102 */
103 public void cluster(double[][] r, int cnum) {
104 /**//*if(cc< cnum)
105 System.err.println("聚类数大于实例数");*/
106 while (cc > cnum) {// 继续聚类，循环直至聚类个数等于cnum
107 int mx = 0, my = 0;
108 double vmin = MAX;
109 for (int i = 0; i < n; i++) { // 寻找最小距离所在的行列
110 for (int j = 0; j < n; j++) {
111 if (j > i) {
112 if (vmin > r[i][j]) {
113 vmin = r[i][j];
114 mx = i;
115 my = j;
116 }
117 }
118 }
119 }
120 ds.union(ds.find(mx), ds.find(my)); // 将最小距离所在的行列实例聚类合并
121 double o1[] = r[mx];
122 double o2[] = r[my];
123 double v[] = new double[n];
124 double vv[] = new double[n];
125 for (int i = 0; i < n; i++) {
126 double tm = Math.min(o1[i], o2[i]);
127 if (tm != 0)
128 v[i] = tm;
129 else
130 v[i] = MAX;
131 vv[i] = MAX;
132 }
133 r[mx] = v;
134 r[my] = vv;
135 for (int i = 0; i < n; i++) { // 更新距离矩阵
136 r[i][mx] = v[i];
137 r[i][my] = vv[i];
138 }
139 cc--;
140 }
141 }
142
143 public static void main(String args[]) {
144 double[][] r = { { 0, 1, 4, 6, 8, 9 }, { 1, 0, 3, 5, 7, 8 },
145 { 4, 3, 0, 2, 4, 5 }, { 6, 5, 2, 0, 2, 3 },
146 { 8, 7, 4, 2, 0, 1 }, { 9, 8, 5, 3, 1, 0 } };
147 Clusterer cl = new Clusterer(6);
148 //cl.cluster(r, 6, 1);
149 cl.cluster(r, 3);
150 cl.output();
151 }
152
153
}
154
3. 小结
层次聚类算法是非常常用的聚类算法，同时也是被广泛研究的聚类算法。层次聚类本身分为合并和分裂两种实现，在合并算法中，又分基于矩阵理论的合并和基于图论的合并。本文只是初学聚类的一点体会，因此只实现了基于矩阵理论的算法，同时，用于大数据集合的层次算法如CURE，ROCK和Chameleon算法都没有涉及，这些算法如果以后有时间，会整理发布。还有截断点的选择，最佳聚类数的确定都是可以研究的问题。
4. 参考文献及推荐阅读
[1]Pattern Recognition Third Edition, Sergios Theodoridis, Konstantinos Koutroumbas
[2]模式识别第三版, Sergios Theodoridis, Konstantinos Koutroumbas著, 李晶皎, 王爱侠, 张广源等译
PS，第四第五节的内容的代码地址：