本文为原创,欢迎转载,转载请注明出处BlogJava。
快速排序的算法思想:
快速排序采用了分治的策略,将原问题分解为若干个规模更小但结构与原问题相似的子问题。用递归方法解决子问题,然后将这些子问题的解组合为原问题的解。
快速排序的程序的一般过程可简单描述为:
1.用统一的方法取得 pivot(轴)。
2.根据pivot 对已有数组进行排序
1) 将array[pivot]存储在tmp变量中,作为比较基准。
以low、high分别从前向后、从后向前遍历数组
2) 从后向前遍历,找到第一个小于tmp的数,将其移动到low的位置。
3) 从前向后遍历,找到第一个大于tmp的数,将其移动到high的位置。
4) 循环2、3步,直到两指针重叠(即退出循环的条件是 low >= high),将tmp移动到low(此时low与high重合)的位置,并将low返回成为新的pivot。
5) 根据4步返回的pivot,对已有数组进行划分,0~pivot-1 和 pivot+1 ~ array.lenght,递归1~5步。直到调用退出。
相信对于以上理论大家一定是耳熟能详了,但理解起来还是比较抽象,下面我就用Excel画图简单的描述一下 快速排序 的过程。
假设我们要写一个程序对已有数组进行排序,简单起见,设定待排序数组为 int[] array = { 4, 2, 1, 7, 5, 3, 8, 6 }。对其用快速排序算法进行排序,过程描述如下:
1.根据已有待排序数组,取得pivot,我在这里取得pivot的策略就是 取 数组的第一个数,这里即为 4。
tmp = 4;
待排序数组:黄色底色表示pivot。
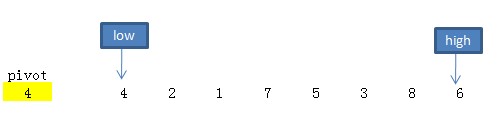
2.从后向前移动high,找到第一个小于tmp的数,则将该数移动到low的位置。

3.从前向后移动low,找到第一个大于tmp(4)的数,将其移动到high的位置。
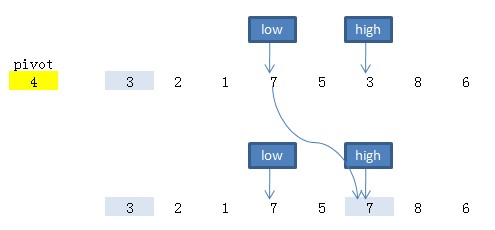
4.然后再向前移动high,试图找到第一个小于tmp(4)的数,但没有找到,此时low与high重叠,将tmp的值放入low的位置,并将low作为pivot返回。
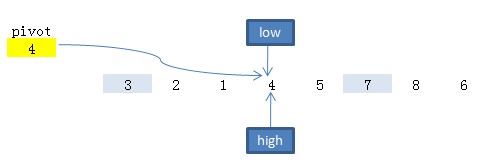
根据新的pivot进行递归调用,将原待排序数组 分解为两块,index区间分别为0~2,4~7,即以下两个子数组
(并未新建数组,只是只关注这个区间的数据,对其进行排序,也就是将问题分解为两个小的子问题,但问题很类似。)

这两个数组的排序过程这里就不画了,一样的过程。
下面来看看实现的代码,与刚刚的过程描述是符合的:
 package com.bz.sort.algorithm;
package com.bz.sort.algorithm;


 public class QuickSort
public class QuickSort  {
{

 /** *//**
/** *//**
 * 对外调用的方法入口。
* 对外调用的方法入口。
 * @param array 待排序数组
* @param array 待排序数组
 */
*/

 public void sort(int[] array)
public void sort(int[] array)  {
{

 if (array == null || array.length < 0)
if (array == null || array.length < 0)  {
{
 throw new RuntimeException("待排序数组中无数据。");
throw new RuntimeException("待排序数组中无数据。");
 }
}

 // 排序
// 排序
 sort(array, 0, array.length - 1);
sort(array, 0, array.length - 1);
 }
}


 /** *//**
/** *//**
 * 快速排序。
* 快速排序。
 * @param arr 待排序数组
* @param arr 待排序数组
 * @param left 关注的区间
* @param left 关注的区间
 * @param right 关注的区间
* @param right 关注的区间
 */
*/

 private void sort(int[] arr, int left, int right)
private void sort(int[] arr, int left, int right)  {
{

 if (left >= right)
if (left >= right)  {
{
 return;
return;
 }
}
 // 取得pivot位置,这里的策略是取得最小的index,即返回left
// 取得pivot位置,这里的策略是取得最小的index,即返回left
 int pivot = findPivot(arr, left, right);
int pivot = findPivot(arr, left, right);
 // 排序并重新计算出pivot
// 排序并重新计算出pivot
 pivot = partion(arr, left, right, pivot);
pivot = partion(arr, left, right, pivot);

 // 以pivot为中心将原数组分解成两块,递归排序
// 以pivot为中心将原数组分解成两块,递归排序
 sort(arr, left, pivot - 1);
sort(arr, left, pivot - 1);
 sort(arr, pivot + 1, right);
sort(arr, pivot + 1, right);
 }
}


 /** *//**
/** *//**
 * 排序并返回新的pivot
* 排序并返回新的pivot
 * @param arr 待排序数组
* @param arr 待排序数组
 * @param left 区间
* @param left 区间
 * @param right 区间
* @param right 区间
 * @param pivot 轴
* @param pivot 轴
 * @return
* @return
 */
*/

 private int partion(int[] arr, int left, int right, int pivot)
private int partion(int[] arr, int left, int right, int pivot)  {
{
 int tmp = arr[pivot];
int tmp = arr[pivot];
 int low = left;
int low = left;
 int high = right;
int high = right;

 while (low < high)
while (low < high)  {
{
 // 从后向前遍历数组,找到第一个小于arr[pivot]的数
// 从后向前遍历数组,找到第一个小于arr[pivot]的数

 while (low < high && tmp < arr[high])
while (low < high && tmp < arr[high])  {
{
 high--;
high--;
 }
}
 arr[low] = arr[high];
arr[low] = arr[high];

 // 从前向后遍历数组,找到第一个大于arr[pivot]的数
// 从前向后遍历数组,找到第一个大于arr[pivot]的数

 while (low < high && tmp >= arr[low])
while (low < high && tmp >= arr[low])  {
{
 low++;
low++;
 }
}
 arr[high] = arr[low];
arr[high] = arr[low];
 }
}

 // 此时low与high重合,将tmp的值移动到low的位置
// 此时low与high重合,将tmp的值移动到low的位置
 arr[low] = tmp;
arr[low] = tmp;
 // 将low当作新的pivot返回
// 将low当作新的pivot返回
 return low;
return low;
 }
}


 /** *//**
/** *//**
 * 取得排序的轴
* 取得排序的轴
 * @param array
* @param array
 * @return
* @return
 */
*/

 protected int findPivot(int[] array, int left, int right)
protected int findPivot(int[] array, int left, int right)  {
{

 if (array == null || array.length < 0)
if (array == null || array.length < 0)  {
{
 throw new RuntimeException("待排序数组中无数据。");
throw new RuntimeException("待排序数组中无数据。");
 }
}
 // 选择第一个元素为轴
// 选择第一个元素为轴
 return left;
return left;
 }
}
 }
}
测试代码如下:
 package com.bz.sort.algorithm;
package com.bz.sort.algorithm;

 import org.junit.Test;
import org.junit.Test;

 import junit.framework.Assert;
import junit.framework.Assert;


 public class QuickSortTest
public class QuickSortTest  {
{
 @Test
@Test

 public void testSort()
public void testSort()  {
{

 int[] array =
int[] array =  { 4, 2, 1, 7, 5, 3, 8, 6 };
{ 4, 2, 1, 7, 5, 3, 8, 6 };
 QuickSort qs = new QuickSort();
QuickSort qs = new QuickSort();
 qs.sort(array);
qs.sort(array);

 for (int i = 0; i < array.length - 1; i++)
for (int i = 0; i < array.length - 1; i++)  {
{
 Assert.assertTrue(array[i] <= array[i + 1]);
Assert.assertTrue(array[i] <= array[i + 1]);
 }
}
 }
}
 }
}

注:此代码只为 演示 排序过程。