近日在CSDN上看到中软一道面试题,挺有意思的。
题目:一条小溪上7块石头,如图所示:
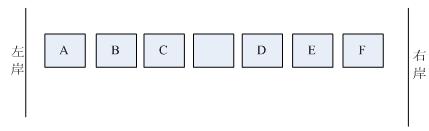
分别有六只青蛙:A,B,C,D,E,F。A,B,C三只蛙想去右岸,它们只会从左向右跳;D,E,F三只蛙想去左岸,它们只会从右向左跳。青蛙每次最多跳到自己前方第2块石头上。请问最少要跳几次所有青蛙上岸。写出步骤。
这个题是个路径搜索的问题,在解空间搜索所有的解,并找出最优的解法(即步骤最少的)。
那么怎么算是一个解呢?具体而言就是最后石头上没有青蛙了。
我们先给题目建模,7块石头,其上可以是没青蛙,可以有一只往左跳的青蛙,也可以有一只往右跳的青蛙。可以把这7块石头看成一个整体,来表示一个状态。这里我们把这7块石头看成一个数组,里面只能有0,1,2三种值,这样表示,那么初始时为:
1,1,1,0,2,2,2
我们把它再表示成一个数字,来表示状态值,这个值把这个数组按三进制拼成一个数字,我们用一个辅助函数来做这件事情:
private final int makeS() {
int r=0;
int p=1;
for(int i=0;i<7;i++)
{
r+=p*states[i];
p*=3;
}
return r;
}
那么题目现在变成从状态111022转换成状态0000000,所需最少的步骤.
那么状态是怎样转换的呢?
很显然。,每次青蛙跳都会触发状态的转换,我们在每个状态时搜索每种可能的转换,我们记初始状态为S(S等于三进制111022)记要求解的值为OPT(S),假如可以转换到t1,t2,...tk.
那么,显然
OPT(S)=min(1+OPT(t1),1+OPT(t2), .,1+OPT(tk));
.,1+OPT(tk));
另外,由于最终状态为0,所以OPT(0)=0,就是说已经在最终状态了,就不需要一步就可以了。
有了上面这个等式,我们可以递归求解了,但是如果单纯的递归,会导致大量的重复计算,所以这里我们用备忘录的方法,记下已经求解出来的OPT(x),放在一个数组里,由于只有7块石头,所以最多我们需要3^7=2187个状态。我们用一个2187个元素的数组, 其中第i个元素表示OPT(i),初始化每个元素用-1表示还未求解。OPT(0) 可直接初始化为0.
到此我们还有一个问题,怎么能够在算法结束的时候打印出最优的步骤呢?按照这个步骤,我们可以重建出青蛙是如何在最优的情况下过河的。为此,我们可以再用一个步骤数组,每次在采取最优步骤的时候记录下来。
整个算法如下:
package test;
import java.util.Arrays;
/**
*
* @author Yovn
*
*/
public class FrogJump {
private int steps[];
private int states[];
private static class Step
{
int offset=-1;
int jump;
int jumpTo;
}
private Step jumps[];
private int initS;
public FrogJump()
{
steps=new int[81*27];
states=new int[7];
for(int i=0;i<3;i++)states[i]=1;
for(int i=4;i<7;i++)states[i]=2;
Arrays.fill(steps, -1);
steps[0]=0;
jumps=new Step[81*27];
initS=makeS();
}
public int shortestSteps(int s)
{
if(steps[s]==-1)
{
int minStep=Integer.MAX_VALUE;
Step oneStep=new Step();
for(int i=0;i<7;i++)
{
if(states[i]==1)
{
if(i>4)
{
states[i]=0;
minStep = recurFind(minStep,oneStep,i,7-i);
states[i]=1;
}
else
{
if(states[i+1]==0)
{
states[i]=0;
states[i+1]=1;
minStep = recurFind(minStep,oneStep,i,1);
states[i]=1;
states[i+1]=0;
}
if(states[i+2]==0)
{
states[i]=0;
states[i+2]=1;
minStep = recurFind(minStep,oneStep,i,2);
states[i]=1;
states[i+2]=0;
}
}
}
else if(states[i]==2)
{
if(i<2)
{
states[i]=0;
minStep = recurFind(minStep,oneStep,i,-1-i);
states[i]=2;
}
else
{
if(states[i-1]==0)
{
states[i]=0;
states[i-1]=2;
minStep = recurFind(minStep,oneStep,i,-1);
states[i]=2;
states[i-1]=0;
}
if(states[i-2]==0)
{
states[i]=0;
states[i-2]=2;
minStep = recurFind(minStep,oneStep,i,-2);
states[i]=2;
states[i-2]=0;
}
}
}
}
steps[s]=minStep;
jumps[s]=oneStep;
}
return steps[s];
}
private final int recurFind(int minStep, Step oneStep, int pos, int jump) {
int toS=makeS();
int r=shortestSteps(toS);
if(r<minStep-1)
{
oneStep.jump=jump;
oneStep.offset=pos;
oneStep.jumpTo=toS;
minStep=r+1;
}
return minStep;
}
public void printPath()
{
int s=initS;
int i=1;
while(s!=0)
{
System.out.println("["+(i++)+"] Frog at #"+jumps[s].offset+" jumps #"+jumps[s].jump);
s=jumps[s].jumpTo;
}
}
private final int makeS() {
int r=0;
int p=1;
for(int i=0;i<7;i++)
{
r+=p*states[i];
p*=3;
}
return r;
}
/**
* @param args
*/
public static void main(String[] args) {
FrogJump fj=new FrogJump();
int steps=fj.shortestSteps(fj.initS);
System.out.println("use "+steps+" steps!");
fj.printPath();
}
}
运行结果:
use 21 steps!
[1] Frog at #2 jumps #1
[2] Frog at #4 jumps #-2
[3] Frog at #5 jumps #-1
[4] Frog at #3 jumps #2
[5] Frog at #1 jumps #2
[6] Frog at #0 jumps #1
[7] Frog at #2 jumps #-2
[8] Frog at #0 jumps #-1
[9] Frog at #4 jumps #-2
[10] Frog at #2 jumps #-2
[11] Frog at #0 jumps #-1
[12] Frog at #5 jumps #2
[13] Frog at #3 jumps #2
[14] Frog at #1 jumps #2
[15] Frog at #5 jumps #2
[16] Frog at #3 jumps #2
[17] Frog at #5 jumps #2
[18] Frog at #6 jumps #-1
[19] Frog at #5 jumps #-2
[20] Frog at #3 jumps #-2
[21] Frog at #1 jumps #-2